Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 19 trang 95 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 19 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình tứ diện ABCD có \(AB \bot \left( {BCD} \right),\)các tam giác BCD và ACD
Đề bài
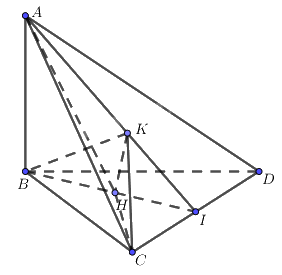
Cho hình tứ diện ABCD có \(AB \bot \left( {BCD} \right),\)các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD. Chứng minh rằng:
a) \(AD \bot CH;\)
b*) \(HK \bot \left( {ACD} \right).\)
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải chi tiết
a) Vì \(AB \bot \left( {BCD} \right),{\rm{ }}CH \subset \left( {BCD} \right) \Rightarrow AB \bot CH.\) Do H là trực tâm của tam giác (BCD) nên \(CH \bot BD.\)
Mà AB, BD cắt nhau trong mặt phẳng (ABD) nên \(CH \bot \left( {ABD} \right).\)
Từ \(CH \bot \left( {ABD} \right),{\rm{ }}AD \subset \left( {ABD} \right) \Rightarrow AD \bot CH.\)
b*) Vì H là trực tâm của tam giác BCD nên \(BH \bot CD.\)
Lại có, \(AB \bot \left( {BCD} \right),{\rm{ }}CD \subset \left( {BCD} \right) \Rightarrow AB \bot CD.\)
Mà AB, BD cắt nhau trong mặt phẳng (ABI) nên \(CD \bot \left( {ABI} \right).\)
Từ \(CD \bot \left( {ABI} \right),{\rm{ }}HK \subset \left( {ABI} \right) \Rightarrow CD \bot HK.\)
Vì K là trực tâm của tam giác ACD nên \(CK \bot AD.\) Mà CK, CH cắt nhau trong mặt phẳng (CHK) nên \(AD \bot \left( {CHK} \right).\)
Lại có, \(AD \bot \left( {CHK} \right),{\rm{ }}HK \subset \left( {CHK} \right) \Rightarrow AD \bot HK.\)
Bên cạnh đó, AD, CD cắt nhau trong mặt phẳng (ACD) nên \(HK \bot \left( {ACD} \right).\)
Bài 19 trang 95 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài tập 19 bao gồm các câu hỏi yêu cầu học sinh tính đạo hàm của các hàm số khác nhau. Các hàm số này có thể là các hàm số đơn giản như đa thức, hàm số lượng giác, hoặc các hàm số phức tạp hơn được tạo thành từ các hàm số đơn giản thông qua các phép toán cộng, trừ, nhân, chia.
Để giải bài tập 19 một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x2 + 3x - 2.
Giải:
f'(x) = (x2)' + (3x)' - (2)'
f'(x) = 2x + 3 - 0
f'(x) = 2x + 3
Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(x) * cos(x).
Giải:
g'(x) = (sin(x))' * cos(x) + sin(x) * (cos(x))'
g'(x) = cos(x) * cos(x) + sin(x) * (-sin(x))
g'(x) = cos2(x) - sin2(x)
Để đạt được kết quả tốt nhất khi giải bài tập 19, bạn cần:
Việc giải bài tập 19 trang 95 Sách bài tập Toán 11 - Cánh Diều không chỉ giúp bạn nắm vững kiến thức về đạo hàm mà còn rèn luyện kỹ năng giải toán, tư duy logic và khả năng áp dụng kiến thức vào thực tế. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong nhiều lĩnh vực khác của cuộc sống.
Giaitoan.edu.vn cam kết cung cấp cho bạn những lời giải chi tiết, dễ hiểu và chính xác nhất cho bài tập 19 trang 95 sách bài tập Toán 11 Cánh Diều và các bài tập khác trong chương trình Toán 11. Hãy truy cập giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích và đồng hành cùng chúng tôi trên con đường chinh phục Toán học!