Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 35 trang 109 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải các bài tập Toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải thích rõ ràng, giúp bạn nắm vững kiến thức và kỹ năng giải Toán.
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng
Đề bài
Cho hai hình bình hành \(ABCD\) và \(ABEF\) không cùng nằm trong một mặt phẳng. Trên các đường chéo \(AC\), \(BF\) lần lượt lấy các điểm \(M\), \(N\) sao cho \(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\). Qua \(M\) vẽ đường thẳng song song với \(AB\) cắt \(AD\) tại \(M'\), qua \(N\) vẽ đường thẳng song song với \(AB\) cắt \(AF\) tại \(N'\).
a) Chứng minh rằng \(\left( {MNN'} \right)\parallel \left( {CDE} \right)\).
b) Gọi \(\left( P \right)\) là mặt phẳng đi qua \(M\) và song song với mặt phẳng \(\left( {AFD} \right)\). Mặt phẳng \(\left( P \right)\) cắt đường thẳng \(EF\) tại \(I\). Tính \(\frac{{FI}}{{FE}}\), biết \(\frac{{AM}}{{AC}} = \frac{1}{3}\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra rằng \(MM'\parallel NN'\), từ đó suy ra 4 điểm \(M\), \(M'\), \(N\), \(N'\) đồng phẳng. Tương tự 4 điểm \(C\), \(D\), \(E\), \(F\) cũng đồng phẳng.
Chứng minh rằng \(NN'\parallel CD\) (do cùng song song với \(AB\)) để suy ra \(NN'\parallel \left( {CDE} \right)\). Tiếp theo, chỉ ra rằng \(M'N'\parallel FD\) để suy ra \(M'N'\parallel \left( {CDE} \right)\), rồi suy ra điều phải chứng minh.
b) Sử dụng định lí Thales: Đường thẳng \(AC\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(A\), \(M\), \(C\). Đường thẳng \(FE\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(F\), \(I\), \(E\). Suy ra \(\frac{{AM}}{{FI}} = \frac{{MC}}{{IE}} = \frac{{CA}}{{EF}}\), từ đó tính được tỉ số \(\frac{{FI}}{{FE}}\).
Lời giải chi tiết
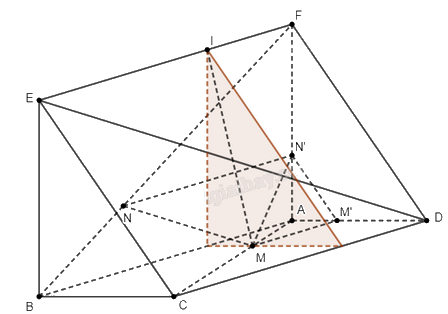
a) Ta có \(MM'\parallel AB\), \(NN'\parallel AB \Rightarrow MM'\parallel NN'\). Suy ra 4 điểm \(M\), \(M'\), \(N\), \(N'\) đồng phẳng. Chứng minh tương tự ta cũng có 4 điểm \(C\), \(D\), \(E\), \(F\) đồng phẳng.
Mặt khác, ta có \(MM'\parallel AB\), \(AB\parallel CD\) nên \(MM'\parallel CD\).
Do \(CD \subset \left( {CDFE} \right)\) nên ta kết luận rằng \(MM'\parallel \left( {CDFE} \right)\).
Hơn nữa, do \(MM'\parallel AB\), nên theo định lí Thales ta có \(\frac{{AM}}{{AC}} = \frac{{AM'}}{{AD}}\).
Chứng minh tương tự ta cũng có \(\frac{{BN}}{{BF}} = \frac{{AN'}}{{AF}}\).
Theo đề bài, vì \(\frac{{AM}}{{AC}} = \frac{{BN}}{{BF}}\), ta suy ra \(\frac{{AM'}}{{AD}} = \frac{{AN'}}{{AF}}\), tức là \(M'N'\parallel FD\).
Do \(FD \subset \left( {CDFE} \right)\) nên ta kết luận rằng \(M'N'\parallel \left( {CDFE} \right)\).
Vì \(MM'\parallel \left( {CDFE} \right)\), \(M'N'\parallel \left( {CDFE} \right)\), \(MM' \cap M'N' = \left\{ {M'} \right\}\), nên ta có \(\left( {MNN'M'} \right)\parallel \left( {CDFE} \right)\), tức là \(\left( {MNN'} \right)\parallel \left( {CDE} \right)\). Bài toán được chứng minh.
b) Ta có \(AD\parallel BE\), \(BC \subset \left( {BCE} \right)\) nên \(AD\parallel \left( {BCE} \right)\). Tương tự ta cũng có \(DF\parallel \left( {BCE} \right)\). Vậy \(\left( {ADF} \right)\parallel \left( {BCE} \right)\)
Theo đề bài, vì \(\left( P \right)\parallel \left( {AFD} \right)\) và \(M \in \left( P \right)\), nên ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\) và \(\left( {BCE} \right)\) đôi một phân biệt, và chúng cũng đôi một song song.
Đường thẳng \(AC\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(A\), \(M\), \(C\). Đường thẳng \(FE\) cắt ba mặt phẳng \(\left( {ADF} \right)\), \(\left( P \right)\), \(\left( {BCE} \right)\) lần lượt tại \(F\), \(I\), \(E\). Áp dụng định lí Thales, ta suy ra \(\frac{{AM}}{{FI}} = \frac{{MC}}{{IE}} = \frac{{CA}}{{EF}} \Rightarrow \frac{{AM}}{{FI}} = \frac{{CA}}{{EF}} \Rightarrow \frac{{AM}}{{AC}} = \frac{{FI}}{{FE}}\).
Mà \(\frac{{AM}}{{AC}} = \frac{1}{3}\), ta kết luận \(\frac{{FI}}{{FE}} = \frac{1}{3}\).
Bài 35 trang 109 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về tích vô hướng của hai vectơ, góc giữa hai vectơ, và các tính chất liên quan để giải quyết các bài toán hình học không gian.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải bài 35 trang 109 sách bài tập Toán 11 - Cánh Diều, bạn cần đọc kỹ đề bài, xác định các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp thông tin về các vectơ, các điểm trong không gian, hoặc các hình khối. Dựa vào đó, bạn cần xác định các vectơ liên quan, tính tích vô hướng của chúng, và sử dụng các công thức để tìm góc giữa chúng hoặc các đại lượng khác.
(Ở đây sẽ là lời giải chi tiết cho bài 35 trang 109, bao gồm các bước giải, các phép tính, và các giải thích rõ ràng. Ví dụ:)
Bài 35: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
Lời giải:
Kết luận: Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng 45°.
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ trong không gian, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 11 - Cánh Diều hoặc các nguồn tài liệu học Toán khác. Hãy luyện tập thường xuyên để nắm vững kiến thức và tự tin giải quyết các bài toán khó hơn.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 35 trang 109 sách bài tập Toán 11 - Cánh Diều. Chúc bạn học tập tốt!