Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 44 trang 45 Sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài tập này một cách cẩn thận, kèm theo các bước giải chi tiết và giải thích rõ ràng.
Lập bảng biến thiên và vẽ đồ thị hàm số:
Đề bài
Lập bảng biến thiên và vẽ đồ thị hàm số:
a) \(y = {\left( {\sqrt 2 } \right)^x};\)
b) \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x};\)
c) \(y = {\log _{\sqrt 3 }}x;\)
d) \(y = - {\log _2}x.\)
Phương pháp giải - Xem chi tiết
Sử dụng các tính chất của lũy thừa với số mũ hữu tỉ để rút gọn biểu thức.
Lời giải chi tiết
a)Vì hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) có cơ số \(\sqrt 2 > 1\) nên ta có bảng biến thiên như sau:
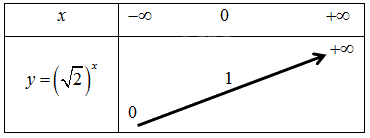
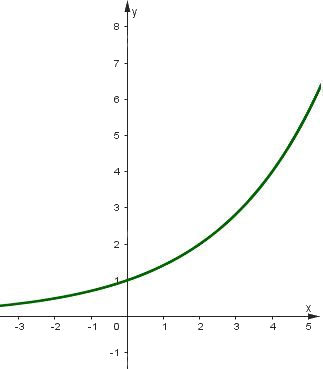
Đồ thị của hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) là một đường cong liền nét đi qua các điểm \(\left( { - 2;\frac{1}{2}} \right),\left( {0;1} \right),\left( {2;2} \right),\left( {4;4} \right).\)
b)Vì hàm số \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x}\) có cơ số \(\frac{1}{{\sqrt 2 }} < 1\) nên ta có bảng biến thiên như sau:
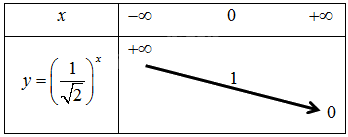
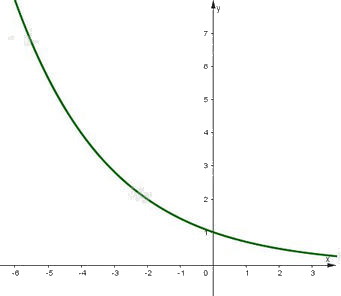
Đồ thị của hàm số \(y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^x}\) là một đường cong liền nét đi qua các điểm \(\left( { - 4;4} \right),\left( { - 2;2} \right),\left( {0;1} \right),\left( {2;\frac{1}{2}} \right).\)
c)Vì hàm số \(y = {\log _{\sqrt 3 }}x\) có cơ số \[\sqrt 3 > 1\] nên ta có bảng biến thiên như sau:
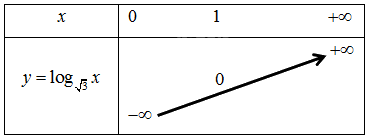
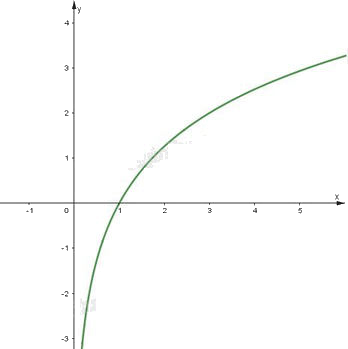
Đồ thị của hàm số \(y = {\log _{\sqrt 3 }}x\) là một đường cong liền nét đi qua các điểm \(\left( {\frac{1}{3}; - 2} \right),\left( {1;0} \right),\left( {3;2} \right),\left( {9;4} \right).\)
d)Vì hàm số \(y = - {\log _2}x\) có cơ số \(2 > 1\) nên ta có bảng biến thiên như sau:
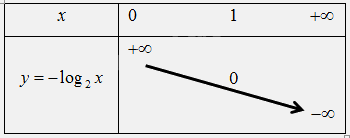
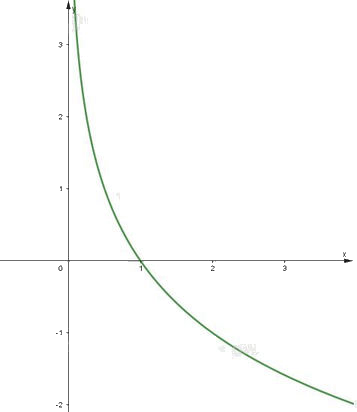
Đồ thị của hàm số \(y = - {\log _2}x\) là một đường cong liền nét đi qua các điểm \(\left( {\frac{1}{2};1} \right),\left( {1;0} \right),\left( {2; - 1} \right),\left( {4; - 2} \right).\)
Bài 44 trang 45 Sách bài tập Toán 11 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này yêu cầu học sinh vận dụng các định lý, tính chất đã học để giải quyết các bài toán liên quan đến quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng.
Bài 44 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giải bài 44 trang 45 Sách bài tập Toán 11 - Cánh Diều hiệu quả, bạn cần nắm vững các kiến thức sau:
Câu a: (Giả sử đề bài là chứng minh hai đường thẳng song song)
Để chứng minh hai đường thẳng song song, ta cần chứng minh chúng cùng song song với một mặt phẳng nào đó. Sử dụng các định lý về đường thẳng song song với mặt phẳng, ta có thể chứng minh hai đường thẳng song song.
(Giải thích chi tiết các bước chứng minh, sử dụng các ký hiệu toán học và hình vẽ minh họa nếu cần thiết)
Câu b: (Giả sử đề bài là chứng minh đường thẳng vuông góc với mặt phẳng)
Để chứng minh một đường thẳng vuông góc với một mặt phẳng, ta cần chứng minh nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Sử dụng các định lý về đường thẳng vuông góc với mặt phẳng, ta có thể chứng minh điều này.
(Giải thích chi tiết các bước chứng minh, sử dụng các ký hiệu toán học và hình vẽ minh họa nếu cần thiết)
Câu c: (Giả sử đề bài là tính góc giữa đường thẳng và mặt phẳng)
Để tính góc giữa đường thẳng và mặt phẳng, ta cần tìm hình chiếu của đường thẳng trên mặt phẳng và sử dụng công thức tính góc.
(Giải thích chi tiết các bước tính toán, sử dụng các ký hiệu toán học và hình vẽ minh họa nếu cần thiết)
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 11 - Cánh Diều hoặc các tài liệu tham khảo khác.
Hy vọng rằng lời giải chi tiết bài 44 trang 45 Sách bài tập Toán 11 - Cánh Diều này sẽ giúp bạn hiểu rõ hơn về các kiến thức liên quan đến đường thẳng và mặt phẳng trong không gian. Chúc bạn học tập tốt!