Bài 54 trang 117 Sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 54 trang 117 Sách bài tập Toán 11 - Cánh Diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Tính:
Đề bài
Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Tính:
a) Khoảng cách giữa hai đường thẳng \(AB\) và \(CD\).
b) Chiều cao và thể tích của khối tứ diện đều \(ABCD\).
c) Côsin của góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\).
d) Côsin của số đo góc nhị diện \(\left[ {C,AB,D} \right]\).
Phương pháp giải - Xem chi tiết
a) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(CD\). Ta chứng minh \(MN\) là đường vuông góc chưng của hai đường thẳng \(AB\) và \(CD\), từ đó khoảng cách cần tìm là đoạn thẳng \(MN\).
b) Gọi \(E\) là hình chiếu của \(A\) trên \(\left( {BCD} \right)\). Ta chứng minh được rằng \(E\) là tâm đường tròn ngoại tiếp của tam giác đều \(BCD\). Từ đó tính được \(BE\), sử dụng định lí Pythagore, ta tính được chiều cao \(AE\) của khối chóp.
Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\), với \(S\) là diện tích đáy, \(h\) là chiều cao của khối chóp.
c) Chứng minh rằng góc giữa \(AB\) và \(\left( {BCD} \right)\) là góc \(\widehat {ABE}\), do đó để tính cosin của góc giữa \(AB\) và \(\left( {BCD} \right)\), ta cần tính \(\cos \widehat {ABE}\).
d) Chứng minh rằng góc \(\widehat {CMD}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {C,AB,D} \right]\). Do vậy, để tính côsin của số đo góc nhị diện \(\left[ {C,AB,D} \right]\), ta tính \(\cos \widehat {CMD}\), và sử dụng định lí cos để tính giá trị này.
Lời giải chi tiết
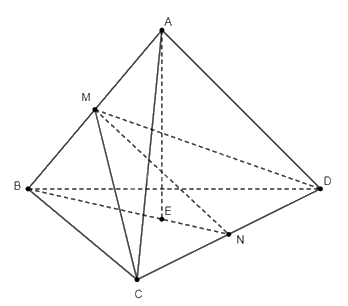
a) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(CD\). Do \(ABCD\) là tứ diện đều, ta suy ra các tam giác \(ABC\), \(ABD\), \(ACD\), \(BCD\) là các tam giác đều.
Tam giác \(ABC\) đều có \(M\) là trung điểm của \(AB\), nên ta có \(CM \bot AB\). Chứng minh tương tự ta có \(DM \bot AB\).
Như vậy, do \(CM \bot AB\), \(DM \bot AB\) nên \(\left( {CDM} \right) \bot AB\), điều này suy ra \(MN \bot AB\). Chứng minh tương tự, ta cũng suy ra \(MN \bot CD\).
Vậy \(MN\) là đường vuông góc chưng của hai đường thẳng \(AB\) và \(CD\), từ đó khoảng cách giữa \(AB\) và \(CD\) là đoạn thẳng \(MN\).
Tam giác \(ABC\) đều cạnh \(a\), đường cao \(CM\) nên ta có \(CM = \frac{{a\sqrt 3 }}{2}\). Tương tự, ta cũng có \(DM = \frac{{a\sqrt 3 }}{2}\)
Vì \(N\) là trung điểm của \(CD\) nên \(CN = \frac{1}{2}CD = \frac{a}{2}\).
Tam giác \(CMN\)vuông tại \(N\), nên\(MN = \sqrt {C{M^2} - C{N^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\).
Vậy khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) bằng \(\frac{{a\sqrt 2 }}{2}\).
b) Gọi \(E\) là hình chiếu của \(A\) trên \(\left( {BCD} \right)\). Ta có \(AE\) là đường cao của tứ diện \(ABCD\).
Do \(ABCD\) là tứ diện đều, nên \(E\) là tâm đường tròn ngoại tiếp của tam giác \(BCD\). Do \(BCD\) là tam giác đều, nên \(E\) cũng là trọng tâm của tam giác \(BCD\). Mà \(N\) là trung điểm của \(CD\), nên ta có \(BE = \frac{2}{3}BN\).
Tam giác \(BCD\) đều cạnh \(a\), đường cao \(BN\) nên ta có \(BN = \frac{{a\sqrt 3 }}{2}\)
Suy ra \(BE = \frac{{a\sqrt 3 }}{2}.\frac{2}{3} = \frac{{a\sqrt 3 }}{3}\).
Tam giác \(ABE\) vuông tại \(E\), nên \(AE = \sqrt {A{B^2} - B{E^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\)
Vậy chiều cao của tứ diện đều là \(\frac{{a\sqrt 6 }}{3}\).
Do đáy \(BCD\) là tam giác đều cạnh \(a\), nên diện tích đáy của tứ diện là \(\frac{{{a^2}\sqrt 3 }}{4}\).
Vậy thể tích của khối tứ diện \(ABCD\) là \(V = \frac{1}{3}Sh = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 6 }}{3} = \frac{{{a^3}\sqrt 2 }}{{12}}\).
c) Do \(E\) là hình chiếu của \(A\) trên \(\left( {BCD} \right)\), nên góc giữa \(AB\) và \(\left( {BCD} \right)\) là góc \(\widehat {ABE}\).
Tam giác \(ABE\) vuông tại \(E\), nên ta có \(\cos \widehat {ABE} = \frac{{BE}}{{AB}} = \frac{{\frac{{a\sqrt 3 }}{3}}}{a} = \frac{{\sqrt 3 }}{3}\).
Vậy côsin góc giữa đường thẳng \(AB\) và mặt phẳng \(\left( {BCD} \right)\) là \(\frac{{\sqrt 3 }}{3}\).
d) Theo câu a, ta có \(CM \bot AB\) và \(DM \bot AB\), nên \(\widehat {CMD}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {C,AB,D} \right]\).
Áp dụng định lí cos trong tam giác \(CMD\), ta có
\(\cos \widehat {CMD} = \frac{{C{M^2} + M{D^2} - C{D^2}}}{{2CM.MD}} = \frac{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} - {a^2}}}{{2.\frac{{a\sqrt 3 }}{2}.\frac{{a\sqrt 3 }}{2}}} = \frac{1}{3}\).
Vậy côsin của số đo góc nhị diện \(\left[ {C,AB,D} \right]\) bằng \(\frac{1}{3}\).
Bài 54 trang 117 Sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về đạo hàm của hàm số. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Dưới đây là đề bài và lời giải chi tiết bài 54 trang 117 Sách bài tập Toán 11 - Cánh Diều:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
f'(x) = 3x2 - 6x
3x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + |
Hàm số f(x) đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
Hàm số f(x) đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
Lưu ý:
Để củng cố kiến thức về đạo hàm và các ứng dụng của đạo hàm, các em có thể tham khảo thêm các bài tập tương tự sau:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 54 trang 117 Sách bài tập Toán 11 - Cánh Diều sẽ giúp các em học sinh hiểu rõ hơn về đạo hàm và tự tin giải các bài tập tương tự. Chúc các em học tốt!