Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 Tập 2 - Cánh Diều. Bài viết này sẽ hướng dẫn bạn giải bài 31 trang 21 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.
Bạn Nam tham gia một trò chơi rút thăm trúng thưởng. Hộp đựng thăm có 50 lá thăm cứng với kích thước và khối lượng như nhau
Đề bài
Bạn Nam tham gia một trò chơi rút thăm trúng thưởng. Hộp đựng thăm có 50 lá thăm cứng với kích thước và khối lượng như nhau, trong đó có 20 lá trúng thưởng, 30 lá không trúng thưởng. Mỗi người được rút 2 lần (sau mỗi lần rút thì ghi kết quả và bỏ lại thăm vào hộp), mỗi lần 2 lá thăm. Nếu rút được 2 lá trúng thưởng thì được 1 tai nghe, nếu rút được 3 lá trúng thưởng thì được 1 tai nghe và 1 bàn phím, nếu rút được 4 lá trúng thưởng thì được 1 máy tính bảng. Tính xác suất để bạn Nam được trúng thưởng có tai nghe (làm tròn kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
- Xác định số phần tử của không gian mẫu.
- Xác định số phần tử của các biến cố.
Lời giải chi tiết
Số phần tử của không gian mẫu là \(n(\Omega ) = C_{50}^2.C_{50}^2\).
Sơ đồ hình cây biểu thị các khả năng thuận lợi của biến cố A:
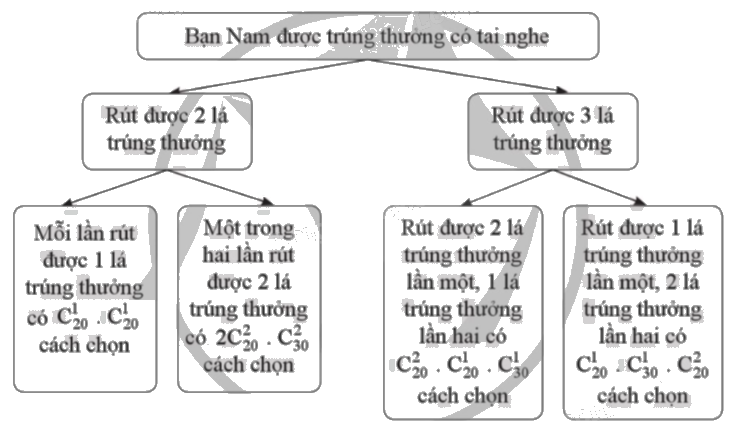
Số kết quả thuận lợi cho biến cố A là:
\(n(A) = C_{20}^1.C_{20}^1 + 2C_{20}^2C_{30}^2 + 2C_{20}^2.C_{20}^1.C_{30}^1 = 393700\).
Xác suất của biến cố A là: \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{393700}}{{C_{50}^2.C_{50}^2}} \approx 0,3\).
Bài 31 trang 21 Sách bài tập Toán 11 Tập 2 - Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 31 thường bao gồm các dạng bài tập sau:
Để giải bài tập 31 trang 21 Sách bài tập Toán 11 Tập 2 - Cánh Diều một cách hiệu quả, bạn cần:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x2 + 2x - 1.
Giải:
f'(x) = d/dx (3x2) + d/dx (2x) - d/dx (1)
f'(x) = 6x + 2 - 0
f'(x) = 6x + 2
Ví dụ 2: Tìm đạo hàm cấp hai của hàm số g(x) = sin(x).
Giải:
g'(x) = cos(x)
g''(x) = d/dx (cos(x))
g''(x) = -sin(x)
Khi tính đạo hàm, bạn cần chú ý đến các quy tắc ưu tiên của các phép toán. Ví dụ, khi tính đạo hàm của tích hai hàm số, bạn cần sử dụng quy tắc đạo hàm của tích.
Để củng cố kiến thức và kỹ năng giải bài tập, bạn có thể tự giải các bài tập sau:
Bài 31 trang 21 Sách bài tập Toán 11 Tập 2 - Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng tính đạo hàm và ứng dụng đạo hàm vào giải quyết các bài toán thực tế. Hy vọng rằng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ tự tin hơn trong quá trình học tập môn Toán.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = c (hằng số) | f'(x) = 0 |
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |