Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 61 trang 118 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 61 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình chóp \(S.ABCD\) đáy là hình bình hành. Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(SB\), \(BC\), \(CD\).
Đề bài
Cho hình chóp \(S.ABCD\) đáy là hình bình hành. Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của \(SB\), \(BC\), \(CD\).
a) Chứng minh rằng \(SC\parallel \left( {MNP} \right)\).
b) Xác định giao tuyến của mặt phẳng \(\left( {MNP} \right)\) với mặt phẳng \(\left( {SCD} \right)\) và giao điểm \(Q\) của đường thẳng \(SD\) với mặt phẳng \(\left( {MNP} \right)\).
c) Xác định giao điểm \(E\) của đường thẳng \(SA\) với mặt phẳng \(\left( {MNP} \right)\).
d) Tính tỉ số \(\frac{{SE}}{{SA}}\).
Phương pháp giải - Xem chi tiết
a) Để chứng minh \(SC\parallel \left( {MNP} \right)\), ta cần chứng minh rằng \(SC\) song song với một đường thẳng nằm trong \(\left( {MNP} \right)\).
b) Gọi \(Q\) là trung điểm của \(SD\). Chứng minh rằng \(Q \in \left( {MNP} \right)\), từ đó suy ra \(PQ\) là giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\), từ đó ta cũng chứng minh được \(Q\) là giao điểm của \(SD\) và \(\left( {MNP} \right)\).
c) Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Trên cạnh \(SA\) lấy \(E\) sao cho \(IE\parallel SC\). Chứng minh rằng \(E \in \left( {MNP} \right)\) và suy ra \(E\) là giao điểm cần tìm.
d) Sử dụng định lí Thales để tính tỉ số \(\frac{{SE}}{{SA}}\).
Lời giải chi tiết
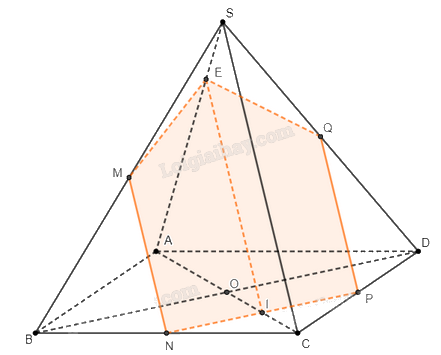
a) Do \(M\) là trung điểm của \(SB\), \(N\) là trung điểm của \(BC\) nên \(MN\) là đường trung bình của tam giác \(SBC\). Suy ra \(MN\parallel SC\).
Vì \(MN \subset \left( {MNP} \right)\) nên \(SC\parallel \left( {MNP} \right)\). Ta có điều phải chứng minh.
b) Gọi \(Q\) là trung điểm của \(SD\). Ta sẽ chứng minh \(PQ\) chính là giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\), và \(Q\) cũng chính là giao điểm của \(SD\) và \(\left( {MNP} \right)\).
Thật vậy, xét hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\), ta có \(P \in CD \subset \left( {SCD} \right)\) và \(P \in \left( {MNP} \right)\), nên giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\) là một đường thẳng đi qua \(P\).
Hơn nữa, do \(MN\parallel SC\), \(SC \subset \left( {SCD} \right)\), \(MN \subset \left( {MNP} \right)\), ta suy ra giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\) là một đường thẳng đi qua \(P\) và song song với \(SC\).
Vì \(P\) là trung điểm của \(CD\), \(Q\) là trung điểm của \(SD\) nên \(PQ\) là đường trung bình của tam giác \(SDC\). Suy ra \(PQ\parallel SC\) và \(PQ\parallel MN\). Do \(PQ\parallel MN\) nên \(Q \in \left( {MNP} \right)\).
Như vậy, \(PQ\) chính là giao tuyến của \(\left( {MNP} \right)\) và \(\left( {SCD} \right)\).
Do \(Q \in \left( {MNP} \right)\) và \(Q \in SD\), ta suy ra \(Q\) là giao điểm của \(SD\) và \(\left( {MNP} \right)\).
c) Gọi \(I\) là giao điểm của \(NP\) và \(AC\). Trên cạnh \(SA\) lấy \(E\) sao cho \(IE\parallel SC\).
Dễ thấy rằng do \(I \in NP\), \(NP \subset \left( {MNP} \right)\) nên \(I \in \left( {MNP} \right)\).
Do \(IE\parallel SC\), \(MN\parallel SC\) , ta suy ra \(IE\parallel MN\). Vì \(I \in \left( {MNP} \right)\), ta suy ra \(E \in \left( {MNP} \right)\).
Như vậy \(E\) là điểm chung của \(SA\) và \(\left( {MNP} \right)\), ta kết luận \(E\) chính là giao điểm của \(SA\) và \(\left( {MNP} \right)\).
d) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Ta có \(P\) là trung điểm của \(CD\), \(N\) là trung điểm của \(BC\) nên \(NP\) là đường trung bình của tam giác \(BCD\). Suy ra \(NP\parallel BD\), hay \(NI\parallel BO\). Do \(N\) là trung điểm của \(BC\), ta kết luận rằng \(I\) là trung điểm của \(OC\), hay \(\frac{{CI}}{{CO}} = \frac{1}{2}\).
Mặt khác, do \(ABCD\) là hình bình hành, \(O\) là giao điểm của \(AC\) và \(BD\), ta suy ra \(O\) là trung điểm của \(AC\), hay \(\frac{{CO}}{{CA}} = \frac{1}{2}\).
Suy ra \(\frac{{CI}}{{CA}} = \frac{{CI}}{{CO}}.\frac{{CO}}{{CA}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\).
Tam giác \(SAC\) có \(IE\parallel SC\), theo định lí Thales ta có \(\frac{{CI}}{{IA}} = \frac{{SE}}{{EA}} \Rightarrow \frac{{CI}}{{CA}} = \frac{{SE}}{{SA}}\).
Như vậy \(\frac{{SE}}{{SA}} = \frac{1}{4}\).
Bài 61 trang 118 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về phép biến hình. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán liên quan đến hình học.
Trước khi đi vào giải chi tiết, chúng ta cần phân tích đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Đồng thời, cần ôn lại các kiến thức cơ bản về các phép biến hình, bao gồm:
(Ở đây sẽ là lời giải chi tiết cho bài 61, bao gồm các bước giải, giải thích rõ ràng và hình vẽ minh họa nếu cần thiết. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm bắt được phương pháp giải bài tập.)
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ xem xét một số ví dụ minh họa. Sau đó, chúng tôi sẽ cung cấp một số bài tập tương tự để bạn luyện tập và củng cố kiến thức.
Ví dụ 1:(Đưa ra một ví dụ tương tự bài 61 và giải chi tiết)
Bài tập 1:(Đưa ra một bài tập tương tự bài 61 để học sinh tự giải)
Kiến thức về các phép biến hình không chỉ quan trọng trong chương trình Toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác như kiến trúc, thiết kế, đồ họa máy tính và robot học. Việc nắm vững các kiến thức này sẽ giúp bạn có một nền tảng vững chắc để học tập và làm việc trong tương lai.
Bài 61 trang 118 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về các phép biến hình. Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trong bài viết này, bạn đã hiểu rõ hơn về cách giải bài tập này và tự tin hơn trong các bài kiểm tra. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải toán.