Giải bài 49 trang 29 Sách bài tập Toán 11 - Cánh Diều

Giải bài 49 trang 29 sách bài tập toán 11 - Cánh diều

Giải bài 49 trang 29 Sách bài tập Toán 11 - Cánh Diều

Bài 49 trang 29 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Số nghiệm của phương trình \(\sin x = 0,3\) trên khoảng \(\left( {0;4\pi } \right)\) là:

Đề bài

Số nghiệm của phương trình \(\sin x = 0,3\) trên khoảng \(\left( {0;4\pi } \right)\) là:

A. 2

B. 3

C. 4

D. 6

Phương pháp giải - Xem chi tiết Giải bài 49 trang 29 sách bài tập toán 11 - Cánh diều 1

Sử dụng đồ thị hàm số \(y = \sin x\) và đường thẳng \(y = 0,3\)

Lời giải chi tiết

Ta có hình vẽ sau

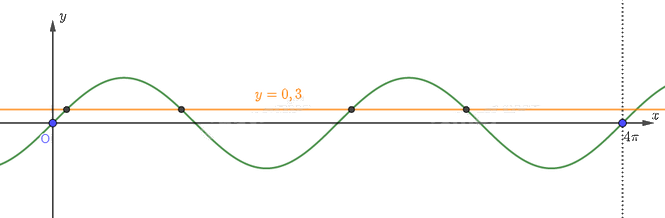
Giải bài 49 trang 29 sách bài tập toán 11 - Cánh diều 2

Nhìn vào hình vẽ, ta thấy đường thẳng \(y = 0,3\) cắt đồ thị \(y = \sin x\) tại 4 điểm có hoành độ ở trên khoảng \(\left( {0;4\pi } \right)\). Có nghĩa là phương trình \(\sin x = 0,3\) có 4 nghiệm ở trên khoảng \(\left( {0;4\pi } \right)\).

Đáp án đúng là C.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 49 trang 29 sách bài tập toán 11 - Cánh diều – hành trang không thể thiếu trong chuyên mục Sách bài tập Toán 11 trên nền tảng tài liệu toán. Bộ bài tập lý thuyết toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 49 trang 29 Sách bài tập Toán 11 - Cánh Diều: Hướng dẫn chi tiết

Bài 49 trang 29 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm. Để giải bài tập này, học sinh cần nắm vững các khái niệm và công thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế.

Phân tích đề bài

Trước khi bắt đầu giải bài tập, chúng ta cần đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 49 trang 29 thường yêu cầu tính đạo hàm của một hàm số hoặc giải một phương trình liên quan đến đạo hàm. Đề bài có thể đưa ra một hàm số cụ thể hoặc yêu cầu học sinh tự xây dựng hàm số dựa trên các thông tin đã cho.

Các bước giải bài tập

Bước 1: Xác định hàm số cần tính đạo hàm. Nếu đề bài cho hàm số, hãy xác định rõ hàm số đó. Nếu đề bài yêu cầu xây dựng hàm số, hãy sử dụng các thông tin đã cho để xây dựng hàm số phù hợp.
Bước 2: Áp dụng các quy tắc tính đạo hàm. Sử dụng các quy tắc tính đạo hàm đã học để tính đạo hàm của hàm số. Lưu ý, cần áp dụng đúng quy tắc cho từng thành phần của hàm số.
Bước 3: Rút gọn biểu thức đạo hàm. Sau khi tính đạo hàm, hãy rút gọn biểu thức đạo hàm để có được kết quả cuối cùng.
Bước 4: Kiểm tra lại kết quả. Sau khi có kết quả, hãy kiểm tra lại kết quả bằng cách thay các giá trị cụ thể vào hàm số và đạo hàm để đảm bảo tính chính xác.

Ví dụ minh họa

Giả sử đề bài yêu cầu tính đạo hàm của hàm số f(x) = x² + 2x + 1. Chúng ta sẽ thực hiện các bước sau:

Bước 1: Hàm số cần tính đạo hàm là f(x) = x² + 2x + 1.
Bước 2: Áp dụng quy tắc tính đạo hàm của tổng và đạo hàm của lũy thừa, ta có: f'(x) = 2x + 2.
Bước 3: Biểu thức đạo hàm đã được rút gọn.
Bước 4: Kiểm tra lại kết quả bằng cách thay x = 0 vào hàm số và đạo hàm. Ta có f(0) = 1 và f'(0) = 2.

Các dạng bài tập thường gặp

Bài 49 trang 29 sách bài tập Toán 11 Cánh Diều có thể xuất hiện dưới nhiều dạng khác nhau, bao gồm:

Tính đạo hàm của hàm số đơn thức.
Tính đạo hàm của hàm số đa thức.
Tính đạo hàm của hàm số lượng giác.
Tính đạo hàm của hàm số mũ và logarit.
Giải phương trình liên quan đến đạo hàm.

Mẹo giải bài tập hiệu quả

Để giải bài tập về đạo hàm hiệu quả, bạn có thể áp dụng một số mẹo sau:

Nắm vững các khái niệm và công thức về đạo hàm.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng các công cụ hỗ trợ tính đạo hàm trực tuyến.
Kiểm tra lại kết quả sau khi giải bài tập.

Ứng dụng của đạo hàm trong thực tế

Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:

Tính vận tốc và gia tốc của vật chuyển động.
Tìm cực trị của hàm số.
Giải quyết các bài toán tối ưu hóa.
Phân tích sự thay đổi của các đại lượng trong tự nhiên và kỹ thuật.

Kết luận

Bài 49 trang 29 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các khái niệm, công thức và quy tắc tính đạo hàm, cùng với việc luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài tập về đạo hàm và ứng dụng kiến thức này vào thực tế.