Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 43 trang 45 Sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 43 trang 45 này với mục tiêu giúp bạn nắm vững kiến thức và kỹ năng giải toán.
Cho ba số thực dương \(a,{\rm{ }}b,{\rm{ }}c\) khác 1
Đề bài
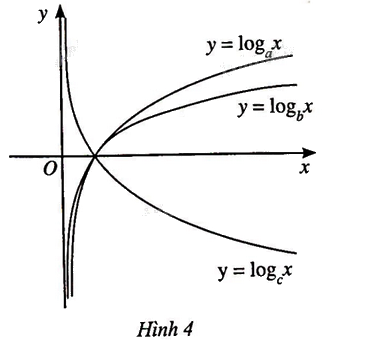
Cho ba số thực dương \(a,{\rm{ }}b,{\rm{ }}c\) khác 1 và đồ thị của ba hàm số loogarit \(y = {\log _a}x,\)\(y = {\log _b}x\) và \(y = {\log _c}x\) được cho bởi Hình 4. Kết luận nào sau đây là đúng đối với ba số\(a,{\rm{ }}b,{\rm{ }}c?\)
A. \(c > b > a.\)
B. \(a > b > c.\)
C. \(b > a > c.\)
D. \(c > a > b.\)
Phương pháp giải - Xem chi tiết
- Hàm số lôgarit \(y = {\log _a}x\) với \(0 < a < 1\) nghịch biến trên \(\left( {0; + \infty } \right).\)
- Hàm số lôgarit \(y = {\log _a}x\) với \(a > 1\) đồng biến trên \(\left( {0; + \infty } \right).\)
Lời giải chi tiết
Hàm số lôgarit \(y = {\log _a}x\) và \(y = {\log _b}x\) đồng biến trên \(\left( {0; + \infty } \right) \Rightarrow a > 1;{\rm{ }}b > 1.\)
Hàm số lôgarit \(y = {\log _c}x\) nghịch biến trên \(\left( {0; + \infty } \right) \Rightarrow 0 < c < 1.\)
Thay \(x = 100 \Rightarrow {\log _a}100 > {\log _b}100 > 0 \Leftrightarrow \frac{1}{{{{\log }_{100}}a}} > \frac{1}{{{{\log }_{100}}b}}\)
\( \Leftrightarrow {\log _{100}}b > {\log _{100}}a \Leftrightarrow b > a > 1.\)
Vậy \(b > a > c.\)
Đáp án C.
Bài 43 trang 45 Sách bài tập Toán 11 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh xác định mối quan hệ giữa các đường thẳng và mặt phẳng, tính góc giữa chúng, và chứng minh các tính chất liên quan.
Bài 43 thường bao gồm các dạng bài tập sau:
Để giải bài tập về đường thẳng và mặt phẳng trong không gian, bạn cần nắm vững các kiến thức sau:
Ngoài ra, bạn cần rèn luyện kỹ năng hình không gian và sử dụng các phương pháp chứng minh hình học.
(Ở đây sẽ là lời giải chi tiết cho từng câu hỏi của bài 43. Ví dụ:)
Câu a: Cho hai đường thẳng a và b. Chứng minh rằng nếu a song song với b thì mọi mặt phẳng chứa a đều song song với b.
Lời giải:
Gọi (P) là mặt phẳng chứa đường thẳng a. Vì a song song với b, nên theo tính chất của hai đường thẳng song song, ta có a và b không có điểm chung. Do đó, b không nằm trong mặt phẳng (P). Nếu (P) cắt b tại một điểm, thì a và b sẽ có điểm chung, điều này mâu thuẫn với giả thiết a song song với b. Vậy (P) song song với b.
Tương tự, mọi mặt phẳng chứa a đều song song với b.
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Khi giải bài tập về đường thẳng và mặt phẳng trong không gian, bạn cần:
Bài 43 trang 45 Sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng giúp bạn hiểu sâu hơn về mối quan hệ giữa đường thẳng và mặt phẳng trong không gian. Hy vọng rằng với lời giải chi tiết và các phương pháp giải bài tập được trình bày trong bài viết này, bạn sẽ tự tin hơn khi giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!