Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 2 trang 9 sách bài tập toán 11 - Cánh diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải bài 2 trang 9 một cách cẩn thận, kèm theo các giải thích rõ ràng, giúp bạn hiểu được bản chất của vấn đề.
Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm như ở Bảng 7 (làm tròn các kết quả đến hàng phần mười).
Đề bài
Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm như ở Bảng 7 (làm tròn các kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải chi tiết
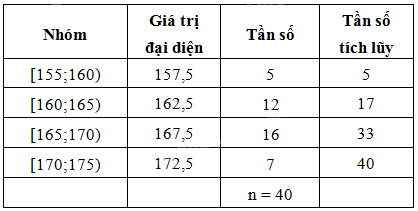
- Chiều cao trung bình của 40 bạn lớp 11A là:
\(\bar x = \frac{{157,5.5 + 162,5.12 + 167,5.16 + 172,5.7}}{{40}} \approx 165,6\left( {{\rm{cm}}} \right).\)
- Ta có: \(\frac{n}{2} = \frac{{40}}{2} = 20\) mà \(17 < 20 < 33.\) Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm [165;170) có \(r = 165,d = 5,{n_3} = 16\) và nhóm 2 là nhóm [160;165) có \(c{f_2} = 17.\)
Trung vị của mẫu số liệu là:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 165 + \left( {\frac{{\frac{{40}}{2} - 17}}{{16}}} \right).5 \approx 165,9\left( {{\rm{cm}}} \right).\)
Tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = {M_e} = 165,9\left( {{\rm{cm}}} \right).\)
- Ta có: \(\frac{n}{4} = \frac{{40}}{4} = 10\) mà \(5 < 10 < 17.\) Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm [160;165) có \(s = 160,{\rm{ }}h = 5,{\rm{ }}{n_2} = 12\) và nhóm 1 là nhóm [155;160) có \(c{f_1} = 5.\)
Tứ phân vị thứ nhất của mẫu số liệu là:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 160 + \left( {\frac{{\frac{{40}}{4} - 5}}{{12}}} \right).5 \approx 162,1\left( {{\rm{cm}}} \right).\)
- Ta có: \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\) mà \(17 < 30 < 33\) Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 3 là nhóm [165;170) có \(t = 165,{\rm{ }}l = 5,{\rm{ }}{n_3} = 16\) và nhóm 2 là nhóm [160;165) có \(c{f_2} = 17.\)
Tứ phân vị thứ ba của mẫu số liệu là:
\({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 165 + \left( {\frac{{\frac{{3.40}}{4} - 17}}{{16}}} \right).5 \approx 169,1\left( {{\rm{cm}}} \right).\)
- Ta thấy: Nhóm 3 ứng với nửa khoảng [165;170) là nhóm có tần số lớn nhất với \(u = 165,{\rm{ }}g = 5,{\rm{ }}{n_3} = 16,{\rm{ }}{n_2} = 12,{\rm{ }}{n_4} = 7.\)
Mốt của mẫu số liệu là:
\({M_0} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 165 + \left( {\frac{{16 - 12}}{{2.16 - 12 - 7}}} \right).5 \approx 166,5\left( {{\rm{cm}}} \right).\)
Bài 2 trang 9 sách bài tập toán 11 - Cánh diều thuộc chương trình học về hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về định nghĩa hàm số, tập xác định, tập giá trị, và các tính chất của hàm số bậc hai để giải quyết các bài toán cụ thể.
Bài 2 trang 9 sách bài tập toán 11 - Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài 2 trang 9 sách bài tập toán 11 - Cánh diều một cách hiệu quả, bạn cần nắm vững các phương pháp sau:
Ví dụ: Cho hàm số y = 2x2 - 4x + 1. Hãy tìm tập xác định, tập giá trị, và đỉnh của parabol.
Giải:
Để củng cố kiến thức về bài 2 trang 9 sách bài tập toán 11 - Cánh diều, bạn nên thực hành giải thêm nhiều bài tập tương tự. Bạn có thể tìm thấy các bài tập này trong sách bài tập, sách tham khảo, hoặc trên các trang web học toán online.
Khi giải bài tập về hàm số bậc hai, bạn cần lưu ý những điều sau:
Bài 2 trang 9 sách bài tập toán 11 - Cánh diều là một bài tập quan trọng giúp bạn hiểu sâu hơn về hàm số bậc hai. Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán liên quan.