Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập toán 11 sách Cánh diều. Bài viết này sẽ hướng dẫn bạn giải bài 4 trang 9 và 10 một cách đầy đủ, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng thời giúp bạn hiểu rõ bản chất của từng bài toán.
Khi thống kê chỉ số đường huyết (đơn vị: mmol/L) của 28 người cao tuổi trong một lần đo, ta được kết quả sau:
Đề bài
Khi thống kê chỉ số đường huyết (đơn vị: mmol/L) của 28 người cao tuổi trong một lần đo, ta được kết quả sau:
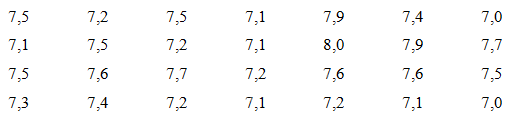
a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với năm nửa khoảng: [7,0;7,2), [7,2;7,4), [7,4;7,6), [7,6;7,8), [7,8;8,0].
b) Độ dài của mỗi nhóm bằng:
A. 7.
B. 8.
C. 1.
D. 0,2.
c) Tần số của nhóm [7,8;8,0] là bao nhiêu?
A. 3.
B. 5.
C. 6.
D. 7.
d) Giá trị \(c{f_3}\) bằng:
A. 7.
B. 13.
C. 20.
D. 25.
e) Giá trị đại diện của nhóm [7,4;7,6) bằng:
A. 7,4.
B. 7,6.
C. 7,5.
D. 2.
g) Nhóm có giá trị đại diện bằng 7,7 là:
A. [7,0;7,2).
B. [7,2;7,4).
C. [7,4;7,6).
D. [7,6;7,8).
Phương pháp giải - Xem chi tiết
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải chi tiết
a) Bảng tần số ghép nhóm cho mẫu số liệu có năm nhóm ứng với năm nửa khoảng:
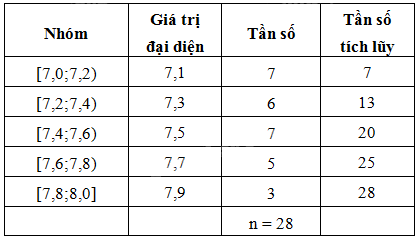
b) Độ dài của mỗi nhóm bằng: 0,2.
Đáp án D.
c) Tần số của nhóm [7,8;8,0] là 3.
Đáp án A.
d) Giá trị \(c{f_3}\) bằng: 20.
Đáp án C.
e) Giá trị đại diện của nhóm [7,4;7,6) bằng: 7,5.
Đáp án C.
g) Nhóm có giá trị đại diện bằng 7,7 là: [7,6;7,8).
Đáp án D.
Bài 4 trong sách bài tập toán 11 Cánh diều tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ và ứng dụng của vectơ trong hình học. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Bài 4 trang 9 thường yêu cầu chứng minh đẳng thức vectơ hoặc tìm tọa độ của một điểm, một vectơ dựa trên các thông tin đã cho. Để giải quyết loại bài này, chúng ta có thể sử dụng các quy tắc cộng, trừ, nhân vectơ với một số thực, cũng như các công thức về tọa độ của vectơ.
Ví dụ: Cho tam giác ABC, tìm vectơ AM sao cho M là trung điểm của BC. Giải: Ta có công thức trung điểm: AM = (AB + AC) / 2. Áp dụng công thức này, ta có thể tìm được tọa độ của vectơ AM.
Bài 4 trang 10 thường liên quan đến việc áp dụng vectơ vào giải quyết các bài toán hình học phẳng, chẳng hạn như chứng minh ba điểm thẳng hàng, chứng minh hai đường thẳng song song hoặc vuông góc. Để giải quyết loại bài này, chúng ta cần sử dụng các điều kiện cần và đủ để ba điểm thẳng hàng, hai đường thẳng song song hoặc vuông góc.
Ví dụ: Chứng minh ba điểm A, B, C thẳng hàng. Giải: Ta cần chứng minh rằng tồn tại một số thực k sao cho AB = kAC. Nếu tìm được k, thì ba điểm A, B, C thẳng hàng.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán online. Việc luyện tập thường xuyên sẽ giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài 4 trang 9, 10 sách bài tập toán 11 - Cánh diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng các kiến thức về vectơ vào giải quyết các bài toán hình học. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải quyết bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!