Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 30 trang 16 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 30 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Trên một mảnh đất hình vuông (ABCD), bác An đặt một chiếc đèn pin tại vị trí (A) chiếu chùm sáng phân kì sang phía góc (C).
Đề bài
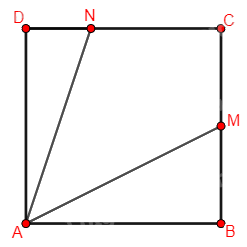
Trên một mảnh đất hình vuông \(ABCD\), bác An đặt một chiếc đèn pin tại vị trí \(A\) chiếu chùm sáng phân kì sang phía góc \(C\). Bác An nhận thấy góc chiếu sáng của đèn pin giới hạn bởi hai tia \(AM\) và \(AN\), ở đó các điểm \(M\), \(N\) lần lượt thuộc các cạnh \(BC\), \(CD\) sao cho \(BM = \frac{1}{2}BC\), \(DN = \frac{1}{3}DC\) (xem hình vẽ).
a) Tính \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right)\).
b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?
Phương pháp giải - Xem chi tiết
a) Sử dụng công thức \(\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\) và công thức tan của góc nhọn trong tam giác vuông.
b) Góc chiếu sáng cần tìm là \(\widehat {MAN}\). Sử dụng kết quả câu a để tính \(\widehat {BAM} + \widehat {DAN}\), từ đó tính được góc \(\widehat {MAN}\).
Lời giải chi tiết
Xét tam giác vuông \(AMB\), ta có \(\tan \widehat {BAM} = \frac{{BM}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{2}\).
Xét tam giác vuông \(AND\), ta có \(\tan \widehat {DAN} = \frac{{ND}}{{AD}} = \frac{{ND}}{{CD}} = \frac{1}{3}\).
Ta có:
\(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right) = \frac{{\tan \widehat {BAM} + \tan \widehat {DAN}}}{{1 - \tan \widehat {BAM}\tan \widehat {DAN}}} = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 - \frac{1}{2}.\frac{1}{3}}} = 1\).
b) Góc chiếu sáng cần tìm là \(\widehat {MAN}\).
Do \(\tan \left( {\widehat {BAM} + \widehat {DAN}} \right) = 1\), nên \(\widehat {BAM} + \widehat {DAN} = {45^o}\).
Suy ra \(\widehat {MAN} = {90^o} - {45^o} = {45^o}\)
Bài 30 trang 16 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về hàm số lượng giác và đồ thị. Để giải quyết bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 30 thường bao gồm các dạng bài tập sau:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng câu hỏi cụ thể trong bài 30. Dưới đây là ví dụ về cách giải một câu hỏi thường gặp:
Ví dụ: Giải phương trình sin(x) = 1/2
Lời giải:
Hàm số lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống và khoa học, bao gồm:
Để củng cố kiến thức, bạn có thể giải thêm các bài tập sau:
Bài 30 trang 16 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hàm số lượng giác và đồ thị. Bằng cách nắm vững kiến thức cơ bản, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.