Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 17 trang 100 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích rõ ràng từng bước để giúp các em học sinh hiểu bài và làm bài tập một cách hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tối đa cho quá trình học tập của các bạn.
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(G\), \(K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD\)
Đề bài
Cho hình chóp tứ giác \(S.ABCD\). Gọi \(G\), \(K\) lần lượt là trọng tâm của các tam giác \(SAB\) và \(SAD\); \(M\), \(N\) lần lượt là trung điểm của các cạnh \(BC\) và \(CD\). Chứng minh rằng \(GK\parallel MN\).
Phương pháp giải - Xem chi tiết
Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\). Chứng minh rằng các đường thẳng \(GK\), \(PQ\), \(BD\), \(MN\) đôi một song song với nhau, từ đó suy ra điều phải chứng minh.
Lời giải chi tiết
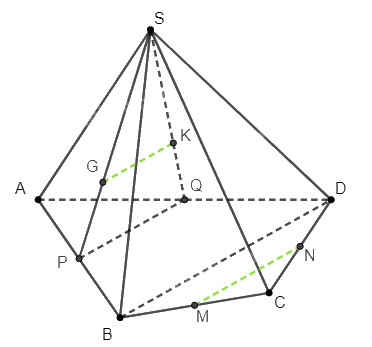
Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\).
Ta có \(G\) là trọng tâm của tam giác \(SAB\), nên suy ra \(G \in SP\) và \(\frac{{SG}}{{SP}} = \frac{2}{3}\).
Chứng minh tương tự ta cũng có \(K \in SQ\) và \(\frac{{SK}}{{SQ}} = \frac{2}{3}\).
Tam giác \(SPQ\) có \(\frac{{SG}}{{SP}} = \frac{{SK}}{{SQ}}\) nên theo định lí Thales ta có \(GK\parallel PQ\).
Xét tam giác \(ABD\), ta có \(P\) là trung điểm của \(AB\), \(Q\) là trung điểm của \(AD\), nên \(PQ\) là đường trung bình của tam giác \(ABD\). Suy ra \(PQ\parallel BD\).
Chứng minh tương tự ta cũng có \(MN\parallel BD\).
Từ đó suy ra \(GK\parallel MN\). Bài toán được chứng minh.
Bài 17 trang 100 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng và các điểm đặc biệt của parabol để giải quyết các bài toán liên quan đến việc tìm phương trình parabol khi biết các yếu tố khác nhau.
Bài 17 bao gồm các câu hỏi và bài tập nhỏ, tập trung vào các kỹ năng sau:
Để giải câu a, ta cần so sánh phương trình (x^2 = 8y) với phương trình chính tắc của parabol (x^2 = 4py). Từ đó suy ra:
Tương tự như câu a, ta so sánh phương trình (y^2 = -6x) với phương trình chính tắc (y^2 = 4px). Từ đó suy ra:
Ngoài các bài tập tìm các yếu tố của parabol, bài 17 còn có thể xuất hiện các dạng bài tập sau:
Để giải bài tập về parabol một cách hiệu quả, các em cần lưu ý những điều sau:
Bài 17 trang 100 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp các em củng cố kiến thức về parabol. Hy vọng với hướng dẫn chi tiết và các lưu ý trên, các em sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc các em học tốt!