Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 62 trang 31 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic và dễ tiếp thu nhất.
Mực nước cao nhất tại một cảng biển là 16 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều xuống thấp thì mực nước thấp nhất là 10 m.
Đề bài
Mực nước cao nhất tại một cảng biển là 16 m khi thuỷ triều lên cao và sau 12 giờ khi thuỷ triều xuống thấp thì mực nước thấp nhất là 10 m. Đồ thị ở hình bên mô tả sự thay đổi chiều cao của mực nước tại cảng trong vòng 24 giờ tính từ lúc nửa đêm. Biết chiều cao của mực nước \(h\) (m) theo thời gian \(t\)(h) \(\left( {0 \le t \le 24} \right)\) được cho bởi công thức \(h = m + a\cos \left( {\frac{\pi }{{12}}t} \right)\) với \(m\), \(a\) là các số thực dương cho trước.
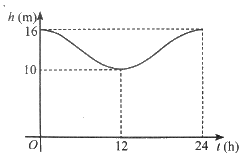
a) Tìm \(m\), \(a\).
b) Tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m.
Phương pháp giải - Xem chi tiết
a) Mực nước thấp nhất đạt được là \(m - a\) khi \(\cos \left( {\frac{\pi }{{12}}t} \right) = - 1\)
Mực nước cao nhất đạt được là \(m + a\) khi \(\cos \left( {\frac{\pi }{{12}}t} \right) = 1\)
Từ đó tìm được \(m\) và \(a\).
b) Với \(m\) và \(a\) tìm được ở câu a, để tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m, ta sẽ giải phương trình ẩn \(t\): \(h = 11,5\) và kết luận.
Lời giải chi tiết
a) Do \( - 1 \le \cos \left( {\frac{\pi }{{12}}t} \right) \le 1 \Rightarrow m - a \le h \le m + a\).
Mực nước thấp nhất đạt được là \(m - a\) (m), mực nước cao nhất đạt được là \(m + a\) (m).
Theo đề bài, ta có hệ phương trình: \(\left\{ \begin{array}{l}m - a = 10\\m + a = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 13\\a = 3\end{array} \right.\)
\( \Rightarrow h = 13 + 3\cos \left( {\frac{\pi }{{12}}t} \right)\)
b) Để tìm thời điểm trong ngày khi chiều cao của mực nước là 11,5 m, ta sẽ giải phương trình: \(h = 11,5 \Leftrightarrow 13 + 3\cos \left( {\frac{\pi }{{12}}t} \right) = 11,5 \Leftrightarrow \cos \left( {\frac{\pi }{{12}}t} \right) = \frac{{ - 1}}{2}\)
\( \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{12}}t = \frac{{2\pi }}{3} + k2\pi \\\frac{\pi }{{12}}t = - \frac{{2\pi }}{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 8 + 24k\\t = - 8 + 24k\end{array} \right.\)\(\left( {k \in \mathbb{Z}} \right)\)
Như vậy, tại thời điểm \(t = 8\)(h) và \(t = 16\)(h), chiều cao của mực nước là 11,5 m.
Bài 62 trang 31 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về hàm số lượng giác. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về các phép biến đổi lượng giác, tính chất của hàm số lượng giác và các phương pháp giải phương trình lượng giác để tìm ra nghiệm.
Bài 62 thường bao gồm các dạng bài tập sau:
Để giải bài 62 trang 31 sách bài tập Toán 11 - Cánh Diều một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Giải phương trình lượng giác sau: 2sin(x) - 1 = 0
Lời giải:
2sin(x) - 1 = 0
2sin(x) = 1
sin(x) = 1/2
x = π/6 + k2π hoặc x = 5π/6 + k2π (k ∈ Z)
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 62 trang 31 sách bài tập Toán 11 - Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt!