Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 19 trang 76 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ cung cấp đáp án, phương pháp giải và các kiến thức liên quan để giúp các em học sinh hiểu rõ hơn về nội dung bài học.
Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu, logic và đầy đủ, giúp các em tự tin hơn trong quá trình học tập và làm bài tập.
Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau
Đề bài
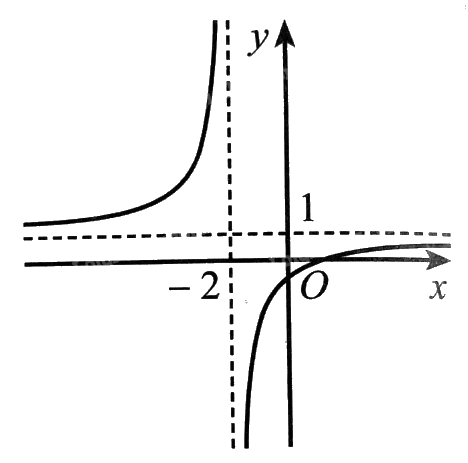
Quan sát đồ thị hàm số ở hình dưới đây và cho biết các giới hạn sau: \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).
Phương pháp giải - Xem chi tiết
Từ đồ thị, để tìm\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right)\), ta cần xác định khi \(x\) dần tới dương vô cực thì \(f\left( x \right)\) dần tới đâu. Tương tự với \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\), \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right)\).
Lời giải chi tiết
Từ đồ thị, ta nhận thấy rằng:
+ Khi \(x\) dần tới dương vô cực thì \(f\left( x \right)\) dần tới 1. Như vậy \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 1\).
+ Khi \(x\) dần tới âm vô cực thì \(f\left( x \right)\) dần tới 1. Như vậy \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 1\).
+ Khi \(x\) dần tới \( - 2\) về bên phải thì \(f\left( x \right)\) dần tới âm vô cực. Như vậy \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = - \infty \).
+ Khi \(x\) dần tới \( - 2\) về bên trái thì \(f\left( x \right)\) dần tới dương vô cực. Như vậy \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right) = + \infty \).
Bài 19 trang 76 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 19 bao gồm một số câu hỏi trắc nghiệm và bài tập tự luận. Các câu hỏi trắc nghiệm thường yêu cầu học sinh lựa chọn đáp án đúng dựa trên việc tính đạo hàm của một hàm số cho trước. Các bài tập tự luận yêu cầu học sinh tính đạo hàm của các hàm số phức tạp hơn, đồng thời giải thích rõ ràng các bước thực hiện.
Để giải bài 19 trang 76 sách bài tập Toán 11 Cánh Diều hiệu quả, học sinh cần:
Ví dụ 1: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Giải:
f'(x) = 3x2 + 4x - 5
Ví dụ 2: Tính đạo hàm của hàm số g(x) = sin(x) * cos(x).
Giải:
g'(x) = cos(x) * cos(x) + sin(x) * (-sin(x)) = cos2(x) - sin2(x)
Khi giải bài tập về đạo hàm, học sinh cần chú ý:
Để học tốt môn Toán 11, học sinh có thể tham khảo các tài liệu sau:
Bài 19 trang 76 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong quá trình học tập và làm bài tập.