Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 37 trang 112 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết mang đến cho bạn những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\).
Đề bài
Cho hình lăng trụ tam giác \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BC\), \(B'C'\). Khẳng định nào sau đây là đúng?
A. \(\left( {A'MN} \right)\parallel \left( {ACC'} \right)\)
B. \(\left( {A'BN} \right)\parallel \left( {AC'M} \right)\)
C. \(C'M\parallel \left( {A'B'B} \right)\)
D. \(BN\parallel \left( {ACC'A'} \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng các tính chất về đường thẳng song song với mặt phẳng, các tính chất về hai mặt phẳng song song.
Lời giải chi tiết
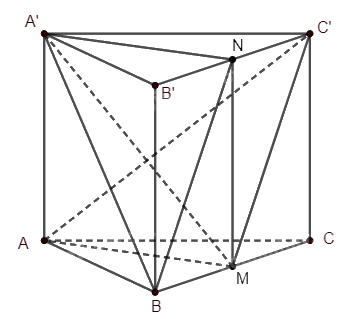
Ta nhận xét rằng \(A' \in \left( {A'MN} \right)\) và \(A' \in \left( {ACC'A'} \right)\), nên hai mặt phẳng \(\left( {A'MN} \right)\) và \(\left( {ACC'} \right)\) có điểm chung, tức là chúng không song song với nhau.
Xét hai mặt phẳng \(\left( {A'BN} \right)\) và \(\left( {AC'M} \right)\). Do \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(B'C'\), nên ta có \(BM = C'N = \frac{1}{2}BC\). Hơn nữa, do \(BC\parallel B'C'\) nên tứ giác \(BMC'N\) là hình bình hành. Suy ra \(BN\parallel C'M\), mà do \(C'M \subset \left( {AC'M} \right)\) nên \(BN\parallel \left( {AC'M} \right)\).
Mặt khác, vì \(M\) và \(N\) lần lượt là trung điểm của \(BC\) và \(B'C'\) nên \(MN\parallel BB'\) và \(MN = BB'\). Do \(ABC.A'B'C'\) là lăng trụ tam giác, nên \(BB'\parallel AA'\) và \(BB' = AA'\). Từ đó ta có \(MN = AA'\) và \(MN\parallel AA'\). Điều này có nghĩa tứ giác \(A'NMA\) là hình bình hành. Suy ra \(A'N\parallel AM\). Do \(AM \subset \left( {AC'M} \right)\) nên \(A'N\parallel \left( {AC'M} \right)\). Vậy \(\left( {A'BN} \right)\parallel \left( {AC'M} \right)\).
Xét mặt phẳng \(\left( {BCC'B'} \right)\), ta thấy rằng \(BB'\) và \(CM\) cắt nhau, mà do \(BB' \subset \left( {A'B'B} \right)\) nên \(CM\) và \(\left( {A'B'B} \right)\) có điểm chung, tức là chúng không song song với nhau.
Chứng minh tương tự, ta cũng suy ra \(BN\) và \(\left( {ACC'A'} \right)\) không song song với nhau.
Đáp án đúng là B.
Bài 37 trang 112 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ, và các ứng dụng trong hình học không gian.
Bài 37 thường bao gồm các dạng bài tập sau:
Để giải bài 37 trang 112 sách bài tập Toán 11 - Cánh Diều, bạn cần thực hiện các bước sau:
Ví dụ minh họa:
Giả sử bài 37 yêu cầu tính góc giữa hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Ta thực hiện như sau:
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 37 trang 112 sách bài tập Toán 11 - Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!