Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 57 trang 118 Sách bài tập Toán 11 Tập 2 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \(O\) là hình chiếu
Đề bài
Cho hình chóp tứ giác đều \(S.ABCD\) có \(AB = a\), \(O\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), \(SO = a\). Gọi \(M\) là hình chiếu của \(O\) trên \(CD\) (xem hình dưới).
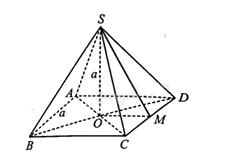
a) Đường thẳng \(AC\) vuông góc với mặt phẳng nào trong các mặt phẳng sau đây?
A. \(\left( {SAB} \right)\)
B. \(\left( {SAD} \right)\)
C. \(\left( {SBC} \right)\)
D. \(\left( {SBD} \right)\)
b) Số đo của góc nhị diện \(\left[ {A,SO,M} \right]\) bằng:
A. \({30^o}\)
B. \({45^o}\)
C. \({135^o}\)
D. \({150^o}\)
c) Khoảng cách giữa hai đường thẳng \(SO\) và \(BC\) bằng:
A. \(a\)
B. \(\frac{a}{2}\)
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \(\frac{{a\sqrt 3 }}{2}\)
d) Thể tích của khối chóp \(S.ABCD\) bằng:
A. \({a^3}\)
B. \(\frac{{{a^3}}}{2}\)
C. \(\frac{{{a^3}}}{3}\)
D. \(3{a^3}\)
e) Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SOM} \right)\) bằng:
A. \(a\)
B. \(\frac{a}{2}\)
C. \(\frac{{a\sqrt 2 }}{2}\)
D. \(\frac{{a\sqrt 3 }}{2}\)
g) Côtang của góc giữa đường thẳng \(SM\) và \(\left( {ABCD} \right)\) bằng:
A. \(\frac{1}{2}\)
B. \(2\)
C. \(1\)
D. \(\frac{{\sqrt 5 }}{5}\)
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về đường thẳng vuông góc với mặt phẳng
b) Xác định góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,M} \right]\).
c) Xác định đường vuông góc chung của hai đường thẳng \(SO\) và \(BC\).
d) Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\), với \(S\) là diện tích đáy và \(h\) là chiều cao của khối chóp đó.
e) Chứng minh rằng \(M\) là hình chiếu của \(C\) trên \(\left( {SOM} \right)\), từ đó khoảng cách cần tính là đoạn thẳng \(CM\).
g) Xác định góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\), rồi tính côtang của góc đó.
Lời giải chi tiết
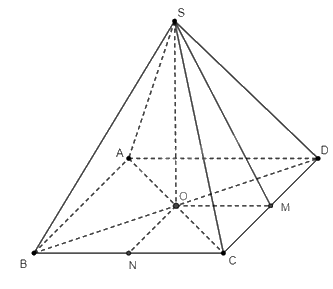
a) Do \(S.ABCD\) là hình chóp tứ giác đều, ta suy ra \(ABCD\) là hình vuông. Điều này suy ra \(AC \bot BD\).
Hơn nữa, do \(SO \bot \left( {ABCD} \right)\) nên \(SO \bot AC\).
Như vậy, do \(AC \bot BD\), \(SO \bot AC\) nên \(AC \bot \left( {SBD} \right)\)
Đáp án đúng là D.
b) Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot AO\) và \(SO \bot OM\). Do đó, góc \(\widehat {AOM}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,M} \right]\).
Do \(M\) là trung điểm của \(CD\), và tam giác \(COD\) vuông cân tại \(O\), ta suy ra \(\widehat {MOD} = {45^o}\) và \(OM \bot CD\). Do đó \(\widehat {AOM} = \widehat {AOD} + \widehat {MOD} = {90^o} + {45^o} = {135^o}\).
Vậy số đo của góc nhị diện \(\left[ {A,SO,M} \right]\) là \({135^o}\).
Đáp án đúng là C.
c) Gọi \(N\) là trung điểm của \(BC\). Tam giác \(OBC\) vuông cân tại \(O\), nên ta có \(ON \bot BC\). Hơn nữa, do \(SO \bot \left( {ABCD} \right)\), nên \(SO \bot ON\).
Vậy \(ON\) là đường vuông góc chung của \(SO\) và \(BC\), do đó khoảng cách giữa hai đường thẳng \(SO\) và \(BC\) là đoạn thẳng \(ON\).
Dễ dàng chứng minh được \(ON = \frac{1}{2}AB = \frac{a}{2}\), vậy khoảng cách giữa hai đường thẳng chéo nhau \(SO\) và \(BC\) bằng \(\frac{a}{2}\).
Đáp án đúng là B.
d) Thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}Sh = \frac{1}{3}A{B^2}.SO = \frac{1}{3}{a^2}.a = \frac{{{a^3}}}{3}\).
Đáp án đúng là C.
e) Do \(SO \bot \left( {ABCD} \right)\), ta suy ra \(SO \bot CM\), mà theo câu b, ta suy ra \(CM \bot OM\).
Từ đó ta có \(CM \bot \left( {SOM} \right)\). Như vậy \(M\) là hình chiếu của \(C\) trên \(\left( {SOM} \right)\), từ đó khoảng cách từ \(C\) đến \(\left( {SOM} \right)\) là đoạn thẳng \(CM\). Do \(CM = \frac{1}{2}CD = \frac{a}{2}\), nên khoảng cách từ \(C\) đến \(\left( {SOM} \right)\) bằng \(\frac{a}{2}\).
Đáp án đúng là B.
g) Do \(O\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\), ta suy ra góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\) là góc \(\widehat {SMO}\).
Ta có \(\cot \widehat {SMO} = \frac{{OM}}{{SO}} = \frac{{\frac{a}{2}}}{a} = \frac{1}{2}\).
Vậy côtang của góc giữa đường thẳng \(SM\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(\frac{1}{2}\).
Đáp án đúng là A.
Bài 57 trang 118 Sách bài tập Toán 11 Tập 2 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào kiến thức về đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng các định lý, tính chất đã học để chứng minh các mối quan hệ hình học, tính toán khoảng cách và góc giữa các đường thẳng, mặt phẳng.
Bài 57 thường bao gồm các dạng bài tập sau:
Để giải quyết các bài tập trong bài 57, bạn cần nắm vững các kiến thức sau:
Bài toán: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập về đường thẳng và mặt phẳng trong không gian, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Hãy chú trọng việc vẽ hình và phân tích đề bài một cách cẩn thận trước khi bắt tay vào giải.
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
Bài 57 trang 118 Sách bài tập Toán 11 Tập 2 - Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải các bài toán về đường thẳng và mặt phẳng trong không gian. Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.