Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 50 trang 117 sách bài tập Toán 11 - Cánh Diều. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu nhất.
Bài viết này sẽ giúp bạn hiểu rõ phương pháp giải bài tập, từ đó nâng cao kỹ năng giải toán và đạt kết quả tốt hơn trong học tập.
Vẽ hình biểu diễn của hình lăng trụ có đáy là tam giác đều.
Đề bài
Vẽ hình biểu diễn của hình lăng trụ có đáy là tam giác đều.
Phương pháp giải - Xem chi tiết
Sử dụng các tính chất của hình biểu diễn của một hình trong không gian.
Lời giải chi tiết
Theo tính chất của hình biểu diễn của một hình trong không gian, ta nhận thấy rằng tam giác bất kỳ có thể xem là hình biểu diễn của tam giác đều. Do đó, hình biểu diễn của hình lăng trụ có đáy là tam giác đều có thể biểu diễn như hình sau.
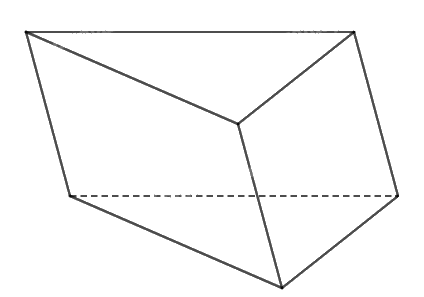
Bài 50 trang 117 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này thường tập trung vào việc vận dụng các kiến thức về biến đổi lượng giác, giải phương trình lượng giác và khảo sát hàm số lượng giác để giải quyết các bài toán thực tế.
Bài tập 50 thường bao gồm các dạng bài sau:
Để giải bài tập 50 trang 117 một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản về hàm số lượng giác, bao gồm:
Dưới đây là lời giải chi tiết cho từng dạng bài tập:
Để xác định tập xác định của hàm số lượng giác, bạn cần tìm các giá trị của x sao cho mẫu số khác 0 và biểu thức trong căn bậc hai lớn hơn hoặc bằng 0.
Để tìm tập giá trị của hàm số lượng giác, bạn cần khảo sát sự biến thiên của hàm số và tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
Để khảo sát sự biến thiên của hàm số lượng giác, bạn cần tính đạo hàm của hàm số và tìm các điểm cực trị. Sau đó, bạn có thể vẽ đồ thị của hàm số để hiểu rõ hơn về sự biến thiên của hàm số.
Để giải phương trình lượng giác, bạn có thể sử dụng các công thức lượng giác cơ bản và các phép biến đổi lượng giác để đưa phương trình về dạng đơn giản hơn. Sau đó, bạn có thể tìm nghiệm của phương trình.
Để ứng dụng hàm số lượng giác vào các bài toán thực tế, bạn cần phân tích bài toán và tìm ra mối liên hệ giữa các đại lượng trong bài toán với hàm số lượng giác. Sau đó, bạn có thể sử dụng hàm số lượng giác để giải quyết bài toán.
Ví dụ: Giải phương trình 2sin(x) - 1 = 0.
Lời giải:
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Bài 50 trang 117 sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải toán lượng giác. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trong bài viết này, bạn sẽ tự tin hơn khi giải quyết các bài tập tương tự.
| Dạng bài | Phương pháp giải |
|---|---|
| Xác định tập xác định | Tìm điều kiện để biểu thức có nghĩa |
| Tìm tập giá trị | Khảo sát hàm số, tìm max, min |