Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 23 trang 95 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra và kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài tập một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho đoạn thẳng AB và mặt phẳng (P) sao cho \(\left( P \right) \bot AB\) và (P)
Đề bài
Cho đoạn thẳng AB và mặt phẳng (P) sao cho \(\left( P \right) \bot AB\) và (P) cắt đoạn thẳng AB tại điểm H thoả mãn HA = 4 cm, HB = 9 cm. Điểm C chuyển động trong mặt phẳng (P) thoả mãn \(\widehat {ACB} = {90^0}.\) Chứng minh rằng điểm C thuộc đường tròn tâm H bán kính 6 cm trong mặt phẳng (P).
Phương pháp giải - Xem chi tiết
Sử dụng hệ thức lượng trong tam giác vuông để tính độ dài HC.
Lời giải chi tiết
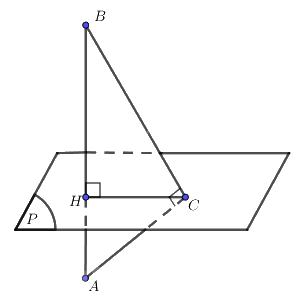
Vì \(AC \bot CB\) nên A, B, C không thẳng hàng.
Ta có: \(\left( P \right) \bot AB,{\rm{ }}HC \subset \left( P \right)\) nên \(AB \bot HC.\)
Xét \(\Delta ABC\) vuông tại C, đường cao CH. Áp dụng hệ thức lượng trong tam giác vuông ta có: \(H{C^2} = HA.HB = 4.9 = 36 \Rightarrow HC = 6\left( {{\rm{cm}}} \right).\)
Vậy C thuộc đường tròn tâm H bán kính 6 cm trong (P).
Bài 23 trang 95 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về hàm số lượng giác. Bài tập này thường tập trung vào việc xác định tính đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác trên một khoảng cho trước. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Trước khi bắt tay vào giải bài tập, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập sẽ yêu cầu tìm khoảng đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải quyết bài toán, ta có thể sử dụng các phương pháp sau:
(Giả sử đề bài cụ thể của bài 23 là: Tìm khoảng đơn điệu của hàm số y = sin(2x) trên khoảng (0, π))
Giải:
1. Tính đạo hàm:
y' = 2cos(2x)
2. Xác định khoảng đơn điệu:
Giải phương trình y' = 0:
2cos(2x) = 0
cos(2x) = 0
2x = π/2 + kπ (k ∈ Z)
x = π/4 + kπ/2 (k ∈ Z)
Xét các nghiệm thuộc khoảng (0, π):
k = 0: x = π/4
k = 1: x = 3π/4
Xét dấu y' trên các khoảng (0, π/4), (π/4, 3π/4), (3π/4, π):
Vậy, hàm số y = sin(2x) đồng biến trên các khoảng (0, π/4) và (3π/4, π), nghịch biến trên khoảng (π/4, 3π/4).
Ngoài bài tập 23, sách bài tập Toán 11 Cánh Diều còn nhiều bài tập tương tự về hàm số lượng giác. Để giải quyết các bài tập này, bạn cần:
Bài 23 trang 95 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số lượng giác. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải quyết bài tập và đạt kết quả tốt trong học tập. Hãy tiếp tục luyện tập và khám phá thêm nhiều kiến thức thú vị khác trên giaitoan.edu.vn!