Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 59 trang 119 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 59 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AB = a\).
Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\) có \(AB = a\).
a) Chứng minh răng \(C'D \bot \left( {BCD'} \right)\), \(BD' \bot C'D\) và \(\left( {BC'D} \right) \bot \left( {BCD'} \right)\).
b) Tính góc giữa hai đường thẳng \(BD\) và \(A'D'\).
c) Tính góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {CDD'C'} \right)\).
d) Tính số đo của góc nhị diện \(\left[ {B,DD',C} \right]\).
e) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {BCD'} \right)\).
g) Chứng minh \(B'C'\parallel \left( {BCD'} \right)\) và tính khoảng cách giữa đường thẳng \(B'C'\) và mặt phẳng \(\left( {BCD'} \right)\).
h) Tính thể tích của khối tứ diện \(C'BCD\) và tính khoảng cách từ điểm \(C\) đến mặt phẳng \(\left( {BC'D} \right)\).
Phương pháp giải - Xem chi tiết
a) Để chứng minh đường thẳng vuông góc với mặt phẳng, ta chứng minh đường thẳng đó vuông góc với 2 đường thẳng bất kỳ cắt nhau trong mặt phẳng.
Để chứng minh 2 mặt phẳng vuông góc, ta cần chỉ là 1 đường thẳng nằm trên mặt phẳng này và vuông góc với mặt phẳng kia.
b) Chỉ ra \(AD\parallel A'D'\), nên góc giữa \(BD\) và \(A'D'\) cũng bằng góc giữa \(BD\) và \(AD\), và bằng \(\widehat {ADB}\).
c) Ta chứng minh \(BC \bot \left( {DCC'D'} \right)\), do đó góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {DCC'D'} \right)\) là góc \(\widehat {BDC}\).
d) Ta chứng minh \(\widehat {BDC}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,DD',C} \right]\).
e) Gọi \(I\) là giao điểm của \(D'C\) và \(DC'\). Theo câu a, ta có \(DI \bot \left( {BCD'} \right)\), từ đó suy ra khoảng cách từ \(D\) đến \(\left( {BCD'} \right)\) là đoạn thẳng \(DI\).
g) Để chứng minh \(B'C'\parallel \left( {BCD'} \right)\), ta chứng minh \(B'C'\) song song với một đường thẳng trong mặt phẳng \(\left( {BCD'} \right)\). Do \(B'C'\parallel \left( {BCD'} \right)\) nên khoảng cách giữa \(B'C'\) và \(\left( {BCD'} \right)\) bằng khoảng cách từ \(C'\) đến \(\left( {BCD'} \right)\).
Theo câu a, ta có \(IC' \bot \left( {BCD'} \right)\), từ đó suy ra \(C'I\) chính là khoảng cách cần tìm.
h) Công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\), với \(S\) là diện tích đáy và \(h\) là chiều cao của khối chóp đó.
Do \(CC' \bot \left( {BCD} \right)\) nên thể tích tứ diện \(C'BCD\) là \(V = \frac{1}{3}CC'.{S_{BCD}}\).
Do thể tích tứ diện \(C'BCD\) cũng có thể được tính bằng công thức \(V = \frac{1}{3}{d_{C,\left( {BC'D} \right)}}.{S_{BC'D}}\), ta suy ra \({d_{C,\left( {BC'D} \right)}} = \frac{{3V}}{{{S_{BC'D}}}}\).
Lời giải chi tiết
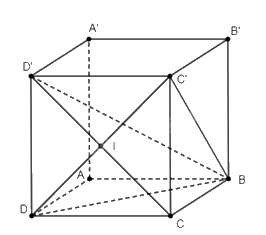
a) Do \(ABCD.A'B'C'D'\) là hình lập phương, nên ta có \(BC \bot \left( {DCC'D'} \right)\), điều này suy ra \(BC \bot C'D\).
Vì \(DCC'D'\) là hình vuông, nên ta có \(C'D \bot CD'\).
Vậy ta có \(BC \bot C'D\), \(C'D \bot CD'\) nên ta có \(C'D \bot \left( {BCD'} \right)\). Ta có điều phải chứng minh.
Do \(C'D \bot \left( {BCD'} \right)\), ta suy ra \(BD' \bot C'D\).
Do \(C'D \bot \left( {BCD'} \right)\), mà \(C'D \subset \left( {BC'D} \right)\),ta suy ra \(\left( {BC'D} \right) \bot \left( {BCD'} \right)\).
b) Dễ thấy rằng do \(ABCD.A'B'C'D'\) là hình lập phương, ta có \(AD\parallel A'D'\), nên góc giữa \(BD\) và \(A'D'\) cũng bằng góc giữa \(BD\) và \(AD\), và bằng \(\widehat {ADB}\).
Do \(ABCD\) là hình vuông, nên \(\widehat {ADB} = {45^o}\).
Vậy góc giữa \(BD\) và \(A'D'\) bằng \({45^o}\).
c) Do \(ABCD.A'B'C'D'\) là hình lập phương, nên ta có \(BC \bot \left( {DCC'D'} \right)\). Điều này suy ra \(C\) là hình chiếu của \(B\) trên \(\left( {DCC'D'} \right)\). Như vậy, góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {DCC'D'} \right)\) là góc \(\widehat {BDC}\).
Do \(ABCD\) là hình vuông, nên \(\widehat {BDC} = {45^o}\).
Vậy góc giữa đường thẳng \(BD\) và mặt phẳng \(\left( {DCC'D'} \right)\) bằng \({45^o}\).
d) Do \(ABCD.A'B'C'D'\) là hình lập phương, ta suy ra \(DD' \bot \left( {ABCD} \right)\). Điều này dẫn tới \(DD' \bot BD\) và \(DD' \bot CD\). Vậy \(\widehat {BDC}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,DD',C} \right]\). Theo câu c, ta có \(\widehat {BDC} = {45^o}\). Vậy số đo của góc nhị diện \(\left[ {B,DD',C} \right]\) bằng \({45^o}\).
e) Gọi \(I\) là giao điểm của \(D'C\) và \(DC'\). Theo câu a, ta có \(C'D \bot \left( {BCD'} \right)\), nên \(DI \bot \left( {BCD'} \right)\). Vậy khoảng cách từ \(D\) đến \(\left( {BCD'} \right)\) là đoạn thẳng \(DI\).
Vì \(DCC'D'\) là hình vuông cạnh \(a\), ta suy ra \(C'D = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \). Suy ra \(DI = C'I = \frac{{C'D}}{2} = \frac{{a\sqrt 2 }}{2}\).
Vậy khoảng cách từ \(D\) đến \(\left( {BCD'} \right)\) bằng \(\frac{{a\sqrt 2 }}{2}\).
g) Do \(ABCD.A'B'C'D'\) là hình lập phương, ta suy ra \(B'C'\parallel BC\).
Mà \(BC \subset \left( {BCD} \right)\) nên ta suy ra \(B'C'\parallel \left( {BCD'} \right)\).
Vì \(B'C'\parallel \left( {BCD'} \right)\), nên khoảng cách giữa \(B'C'\) và \(\left( {BCD'} \right)\) cũng bằng khoảng cách từ \(C'\) đến \(\left( {BCD'} \right)\).
Theo câu a, ta có \(C'D \bot \left( {BCD'} \right)\), điều này cũng có nghĩa \(C'I \bot \left( {BCD'} \right)\), tức khoảng cách từ \(C'\) đến \(\left( {BCD'} \right)\) là đoạn thẳng \(C'I\). Mà theo câu e, vì \(C'I = \frac{{a\sqrt 2 }}{2}\), ta kết luận rằng khoảng cách giữa \(B'C'\) và \(\left( {BCD'} \right)\) bằng \(\frac{{a\sqrt 2 }}{2}\).
h) Do \(CC' \bot \left( {BCD} \right)\) nên thể tích tứ diện \(C'BCD\) là
\(V = \frac{1}{3}CC'.{S_{BCD}} = \frac{1}{3}CC'.\frac{{BC.CD}}{2} = \frac{{a.a.a}}{6} = \frac{{{a^3}}}{6}\).
Tam giác \(BC'D\) có \(BC' = C'D = BD = a\sqrt 2 \) (do chúng đều là đường chéo của các mặt của hình lập phương) nên tam giác đó đều.
Diện tích tam giác \(BC'D\) bằng \({S_{BC'D}} = \frac{{B{D^2}\sqrt 3 }}{4} = \frac{{{{\left( {a\sqrt 2 } \right)}^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{2}\).
Vì thể tích tứ diện \(C'BCD\) cũng có thể được tính bằng công thức \(V = \frac{1}{3}{d_{C,\left( {BC'D} \right)}}.{S_{BC'D}}\), ta suy ra \({d_{C,\left( {BC'D} \right)}} = \frac{{3.\frac{{{a^3}}}{6}}}{{\frac{{{a^2}\sqrt 3 }}{2}}} = \frac{{a\sqrt 3 }}{3}\).
Vậy khoảng cách từ \(C\) đến mặt phẳng \(\left( {BC'D} \right)\) bằng \(\frac{{a\sqrt 3 }}{3}\).
Bài 59 trang 119 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về đạo hàm. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Trước khi bắt đầu giải bài, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Điều này giúp bạn lựa chọn phương pháp giải phù hợp và tránh sai sót không đáng có.
(Ở đây sẽ là lời giải chi tiết cho bài 59, bao gồm các bước giải, giải thích rõ ràng từng bước, và các lưu ý quan trọng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh dễ dàng theo dõi và nắm bắt.)
Để giúp bạn hiểu rõ hơn về cách giải bài 59, chúng tôi sẽ cung cấp một ví dụ minh họa cụ thể. Ví dụ này sẽ giúp bạn áp dụng các kiến thức đã học vào thực tế và tự tin hơn trong việc giải các bài toán tương tự.
Ngoài bài 59, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 Cánh Diều. Dưới đây là một số dạng bài tập thường gặp:
Để giải bài tập đạo hàm một cách hiệu quả, bạn có thể áp dụng một số mẹo sau:
Bài 59 trang 119 sách bài tập Toán 11 Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc học Toán 11.
| Hàm số y = f(x) | Đạo hàm y' = f'(x) |
|---|---|
| C (hằng số) | 0 |
| xn | nxn-1 |
| sin x | cos x |
| cos x | -sin x |
| tan x | 1/cos2x |
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!