Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 6 trang 10 sách bài tập Toán 11 - Cánh diều. Bài viết này sẽ giúp bạn nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn học toán hiệu quả và đạt kết quả cao.
Cho lục giác đều \(ABCDEF\)nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều ngược chiều kim đồng hồ).
Đề bài
Cho lục giác đều \(ABCDEF\)nội tiếp trong đường tròn lượng giác (thứ tự đi từ \(A\) đến các đỉnh theo chiều ngược chiều kim đồng hồ). Tính số đo của các góc lượng giác \(\left( {OA,OB} \right)\), \(\left( {OA,OC} \right)\), \(\left( {OA,OD} \right)\), \(\left( {OA,OE} \right)\), \(\left( {OA,OF} \right)\).
Phương pháp giải - Xem chi tiết
Do lục giác đều \(ABCDEF\) nội tiếp trong đường tròn lượng giác tâm \(O\), nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\)
Sử dụng hệ thức Chasles để tính số đo của các góc lượng giác \(\left( {OA,OB} \right)\),\(\left( {OA,OC} \right)\), \(\left( {OA,OD} \right)\), \(\left( {OA,OE} \right)\), \(\left( {OA,OF} \right)\)
Lời giải chi tiết
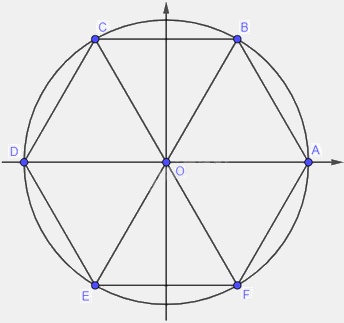
Vì lục giác đều \(ABCDEF\) nội tiếp đường tròn lượng giác tâm \(O\), nên ta có 6 góc bằng nhau: \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = {60^o} = \frac{\pi }{3}\)
Do \(\widehat {AOB} = \frac{\pi }{3} \Rightarrow \left( {OA,OB} \right) = \frac{\pi }{3} + k2\pi \).
Áp dụng hệ thức Chasles, ta có:
\(\left( {OA,OC} \right) = \left( {OA,OB} \right) + \left( {OB,OC} \right) + k2\pi = \frac{\pi }{3} + \frac{\pi }{3} + k2\pi = \frac{{2\pi }}{3} + k2\pi \)
\(\left( {OA,OD} \right) = \left( {OA,OC} \right) + \left( {OC,OD} \right) + k2\pi = \frac{{2\pi }}{3} + \frac{\pi }{3} + k2\pi = \pi + k2\pi \)
\(\left( {OA,OE} \right) = \left( {OA,OD} \right) + \left( {OD,OE} \right) + k2\pi = \pi + \frac{\pi }{3} + k2\pi = \frac{{4\pi }}{3} + k2\pi = - \frac{{2\pi }}{3} + k2\pi \)
\(\left( {OA,OF} \right) = \left( {OA,OE} \right) + \left( {OE,OF} \right) + k2\pi = - \frac{{2\pi }}{3} + \frac{\pi }{3} + k2\pi = - \frac{\pi }{3} + k2\pi \)
Bài 6 trang 10 sách bài tập Toán 11 - Cánh diều thuộc chương trình học về hàm số lượng giác. Bài tập này tập trung vào việc vận dụng các kiến thức về đồ thị hàm số lượng giác, đặc biệt là hàm số sin, cosin, tang và cotang để giải quyết các bài toán thực tế. Việc nắm vững các tính chất của đồ thị hàm số lượng giác là yếu tố then chốt để giải quyết bài tập này một cách hiệu quả.
Bài 6 trang 10 sách bài tập Toán 11 - Cánh diều thường bao gồm các dạng bài tập sau:
Để giải bài 6 trang 10 sách bài tập Toán 11 - Cánh diều một cách hiệu quả, bạn cần thực hiện theo các bước sau:
Ví dụ 1: Xác định biên độ, chu kỳ, pha ban đầu và các điểm đặc biệt của đồ thị hàm số y = 2sin(x - π/3).
Giải:
Khi giải bài tập về hàm số lượng giác, bạn cần lưu ý những điều sau:
Để học tập và ôn luyện kiến thức về hàm số lượng giác, bạn có thể tham khảo các tài liệu sau:
Bài 6 trang 10 sách bài tập Toán 11 - Cánh diều là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số lượng giác. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc bạn học tập tốt!