Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 45 trang 113 sách bài tập Toán 11 - Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi luôn cố gắng trình bày lời giải một cách rõ ràng, logic, kèm theo các ví dụ minh họa để bạn dễ dàng tiếp thu. Hãy cùng bắt đầu nhé!
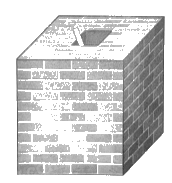
Phần trong của một bể đựng nước được xây có dạng hình hộp như hình dưới đây. Để xác định tỉ số của độ cao mực nước trong bể với chiều cao của lòng bể
Đề bài
Phần trong của một bể đựng nước được xây có dạng hình hộp như hình dưới đây. Để xác định tỉ số của độ cao mực nước trong bể với chiều cao của lòng bể, bạn Minh làm như sau: “Lấy một thanh thước thẳng đủ dài cắm vào bể sao cho một đầu chạm đáy bể và để thước tựa vào mép dưới của thành miệng bể, đánh dấu điểm tựa. Sau đó rút thước lên, tính tỉ số độ dài của phần thước chìm trong nước và độ dài của phần thước từ điểm được đánh dấu đến điểm đầu chạm đáy bể. Tỉ số đó chính bằng tỉ số của độ cao mực nước trong bể với chiều cao lòng bể”. Bạn Minh làm có đúng không? Vì sao?
Phương pháp giải - Xem chi tiết
Sử dụng định lí Thales trong không gian để chỉ ra rằng cách làm của bạn Nam là đúng hay sai.
Lời giải chi tiết
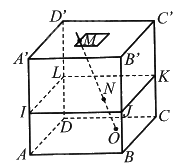
Giả sử phần trong bể nước và thước được biểu diễn bởi hình hộp \(ABCD.A'B'C'D'\) và đường thẳng \(MO\). Mặt nước được biểu diễn bởi mặt phẳng \(\left( {IJKL} \right)\). Khi đó, ba mặt phẳng \(\left( {ABCD} \right)\), \(\left( {IJKL} \right)\), \(\left( {A'B'C'D'} \right)\) là ba mặt phẳng song song. Nhận xét rằng hai đường thẳng \(AA'\) và \(MO\) cùng cắt 3 mặt phẳng \(\left( {ABCD} \right)\), \(\left( {IJKL} \right)\), \(\left( {A'B'C'D'} \right)\) nên theo định lí Thales trong không gian, ta có: \(\frac{{A'I}}{{MN}} = \frac{{IA}}{{NO}} = \frac{{AA'}}{{OM}} \Rightarrow \frac{{IA}}{{AA'}} = \frac{{NO}}{{OM}}\).
Như vậy, bạn Minh làm như vậy là đúng.
Bài 45 trang 113 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này thường tập trung vào việc vận dụng các kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ, và các ứng dụng trong hình học không gian.
Bài 45 thường bao gồm các dạng bài tập sau:
Để giải câu a, ta cần xác định tọa độ của các vectơ liên quan. Sau đó, áp dụng công thức tính tích vô hướng và sử dụng công thức tính góc giữa hai vectơ để tìm ra kết quả.
Ví dụ:
| Bước | Thực hiện | Kết quả |
|---|---|---|
| 1 | Xác định tọa độ vectơ a và b | a = (x1, y1, z1), b = (x2, y2, z2) |
| 2 | Tính tích vô hướng a.b | a.b = x1*x2 + y1*y2 + z1*z2 |
| 3 | Tính độ dài của vectơ a và b | |a| = √(x1^2 + y1^2 + z1^2), |b| = √(x2^2 + y2^2 + z2^2) |
| 4 | Tính cos(θ) | cos(θ) = (a.b) / (|a||b|) |
| 5 | Tìm θ | θ = arccos(cos(θ)) |
Câu b thường yêu cầu kiểm tra tính vuông góc của hai vectơ. Để làm điều này, ta chỉ cần tính tích vô hướng của hai vectơ đó. Nếu tích vô hướng bằng 0, thì hai vectơ vuông góc.
Ví dụ:
Cho hai vectơ a = (1, 2, 3) và b = (4, -5, 6). Tính a.b:
a.b = 1*4 + 2*(-5) + 3*6 = 4 - 10 + 18 = 12
Vì a.b ≠ 0, nên hai vectơ a và b không vuông góc.
Bài 45 trang 113 sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về tích vô hướng của hai vectơ. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải quyết bài tập một cách hiệu quả. Chúc bạn học tốt!