Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 27 trang 21 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra và kỳ thi.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 27 trang 21 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Người ta ghi lại tốc độ của 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi lại tốc độ của 40 xe đó (đơn vị: km/h):
Đề bài
Người ta ghi lại tốc độ của 40 xe đạp đi qua một vị trí trên đường. Mẫu số liệu dưới đây ghi lại tốc độ của 40 xe đó (đơn vị: km/h):
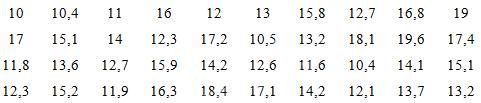
a) Lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy có năm nhóm ứng với năm nửa khoảng: [10 ; 12), [12 ; 14), (14 ; 16), [16 ; 18), [18 ; 20).
b) Xác định các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm trên (làm tròn các kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Áp dụng các công thức đã học để xác định các đại lượng tiêu biểu.
Lời giải chi tiết
a) Bảng tần số ghép nhóm cho mẫu số liệu có năm nhóm ứng với năm nửa khoảng
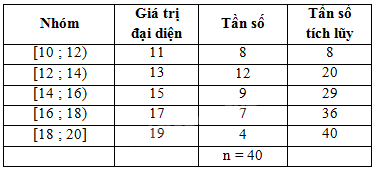
- Tốc độ trung bình của 40 xe đạp là:
\(\bar x = \frac{{11.8 + 13.12 + 15.9 + 17.7 + 19.4}}{{40}} \approx 14,4\) (km/h).
- Ta có: \(\frac{n}{2} = \frac{{40}}{2} = 20\) mà \(20 = 20 < 29.\) Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.
Xét nhóm 3 là nhóm [14 ; 16) có \(r = 14,{\rm{ }}d = 2,{\rm{ }}{n_3} = 9\) và nhóm 2 là nhóm
[12 ; 14) có \(c{f_2} = 20.\)
Trung vị của mẫu số liệu là:
\({M_e} = r + \left( {\frac{{\frac{n}{2} - c{f_{k - 1}}}}{{{n_k}}}} \right).d = 14 + \left( {\frac{{20 - 20}}{9}} \right).2 = 14\) (km/h).
Tứ phân vị thứ hai của mẫu số liệu là: \({Q_2} = {M_e} = 14\) (km/h).
- Ta có: \(\frac{n}{4} = \frac{{40}}{4} = 10\) mà \(8 < 10 < 13.\) Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.
Xét nhóm 2 là nhóm [12 ; 14) có \(s = 12,{\rm{ }}h = 2,{\rm{ }}{n_2} = 12\) và nhóm 1 là nhóm
[10 ; 12) có \(c{f_1} = 8.\)
Tứ phân vị thứ nhất của mẫu số liệu là:
\({Q_1} = s + \left( {\frac{{\frac{n}{4} - c{f_{p - 1}}}}{{{n_p}}}} \right).h = 12 + \left( {\frac{{10 - 8}}{{12}}} \right).2 = 12,3\) (km/h).
- Ta có: \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\) mà \(29 < 30 < 36.\) Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.
Xét nhóm 4 là nhóm [16 ; 18) có \(t = 16,{\rm{ }}l = 2,{\rm{ }}{n_4} = 7\) và nhóm 3 là nhóm
[14 ; 16) có \(c{f_3} = 29.\)
Tứ phân vị thứ ba của mẫu số liệu là:
\({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} - c{f_{q - 1}}}}{{{n_q}}}} \right).l = 16 + \left( {\frac{{30 - 29}}{7}} \right).2 \approx 16,3\)(km/h).
- Ta thấy: Nhóm 2 ứng với nửa khoảng [12 ; 14) là nhóm có tần số lớn nhất với \(u = 12,{\rm{ }}g = 2,{\rm{ }}{n_2} = 12,{\rm{ }}{n_1} = 8,{\rm{ }}{n_3} = 9.\)
Mốt của mẫu số liệu là:
\({M_0} = u + \left( {\frac{{{n_i} - {n_{i - 1}}}}{{2{n_i} - {n_{i - 1}} - {n_{i + 1}}}}} \right).g = 12 + \left( {\frac{{12 - 8}}{{2.12 - 8 - 9}}} \right).2 \approx 13,1\) (km/h).
Bài 27 trang 21 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này tập trung vào việc vận dụng các kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ, và các ứng dụng trong hình học.
Bài 27 bao gồm các dạng bài tập sau:
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 27 trang 21 sách bài tập Toán 11 Cánh Diều:
Cho hai vectơ a và b có |a| = 3, |b| = 4 và góc giữa chúng là 60°. Tính a.b.
Lời giải:
a.b = |a||b|cos(60°) = 3 * 4 * 0.5 = 6
Cho hai vectơ a = (1; 2) và b = (-3; 1). Tính a.b.
Lời giải:
a.b = 1*(-3) + 2*1 = -3 + 2 = -1
Cho tam giác ABC có AB = 5, AC = 8 và góc BAC = 60°. Tính độ dài BC.
Lời giải:
Áp dụng định lý cosin trong tam giác ABC, ta có:
BC2 = AB2 + AC2 - 2*AB*AC*cos(BAC) = 52 + 82 - 2*5*8*cos(60°) = 25 + 64 - 80*0.5 = 89 - 40 = 49
BC = √49 = 7
Để giải tốt các bài tập về tích vô hướng, bạn cần nắm vững các công thức và tính chất sau:
Để củng cố kiến thức và kỹ năng giải bài tập về tích vô hướng, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 Cánh Diều và các tài liệu học tập khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn chi tiết hơn.
Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, bạn đã hiểu rõ cách giải bài 27 trang 21 sách bài tập Toán 11 Cánh Diều. Chúc bạn học tập tốt và đạt kết quả cao trong các kỳ thi!