Chào mừng các em học sinh đến với lời giải chi tiết bài 45 trang 109, 110 sách bài tập Toán 11 Cánh Diều. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải từng bước một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin làm bài tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp tài liệu học tập chất lượng và giải pháp học tập hiệu quả.
Cho hình chữ nhật \(ABCD\) có \(AB = 3a\), \(AD = 4a\).
Đề bài
Cho hình chữ nhật \(ABCD\) có \(AB = 3a\), \(AD = 4a\).
a) Khoảng cách từ điểm \(A\) đến đường thẳng \(BC\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
b) Khoảng cách từ điểm \(A\) đến đường thẳng \(BD\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
c) Khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) bằng:
A. \(2,4a\)
B. \(3a\)
C. \(4a\)
D. \(5a\)
Phương pháp giải - Xem chi tiết
Khoảng cách từ 1 điểm đến 1 đường thẳng là độ dài đoạn thẳng nối điểm đó và hình chiếu của nó trên đường thẳng.
Khoảng cách giữa 2 đường thẳng song song là khoảng cách từ 1 điểm của đường thẳng này đến đường thẳng kia.
Lời giải chi tiết
a) Do \(ABCD\) là hình chữ nhật, nên ta có \(AB \bot BC\). Như vậy khoảng cách từ điểm \(A\) đến đường thẳng \(BC\) là đoạn thẳng \(AB\). Do \(AB = 3a\), nên đáp án cần chọn là đáp án B.
b) Gọi \(H\) là hình chiếu của \(A\) trên \(BD\). Khi đó khoảng cách từ \(A\) đến \(BD\) là đoạn thẳng \(AH\).
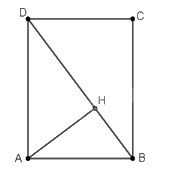
Tam giác \(ABD\) vuông tại \(A\), đường cao \(AH\) nên ta có \(BD = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\)
Như vậy \(AH = \frac{{AB.AD}}{{BD}} = \frac{{3a.4a}}{{5a}} = 2,4a\).
Đáp án cần chọn là đáp án A.
c) Do \(AB\parallel CD\) nên khoảng cách giữa 2 đường thẳng này chính là khoảng cách từ điểm \(A\) đến đường thẳng \(CD\). Vì \(AD \bot DC\) nên khoảng cách giữa hai đường thẳng \(AB\) và \(CD\) chính là đoạn thẳng \(AD\). Mà \(AD = 4a\), nên đáp án đúng là đáp án C.
Bài 45 thuộc chương trình Toán 11, sách bài tập Cánh Diều, tập trung vào việc ôn tập chương 3: Hàm số lượng giác và đồ thị. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học về hàm số lượng giác, các phép biến đổi lượng giác, và đồ thị hàm số lượng giác để giải quyết các bài toán cụ thể.
Bài 45 bao gồm các dạng bài tập sau:
Đề bài: Xác định tập xác định của hàm số y = tan(2x + π/3).
Lời giải: Hàm số y = tan(2x + π/3) xác định khi và chỉ khi 2x + π/3 ≠ π/2 + kπ, với k là số nguyên. Từ đó, ta có 2x ≠ π/6 + kπ, suy ra x ≠ π/12 + kπ/2, với k là số nguyên. Vậy tập xác định của hàm số là D = R \ {π/12 + kπ/2, k ∈ Z}.
Đề bài: Tìm tập giá trị của hàm số y = 2sin(x) + 1.
Lời giải: Vì -1 ≤ sin(x) ≤ 1, nên -2 ≤ 2sin(x) ≤ 2. Do đó, -1 ≤ 2sin(x) + 1 ≤ 3. Vậy tập giá trị của hàm số là [-1, 3].
Đề bài: Xét tính chẵn, lẻ của hàm số y = cos(x) + sin(x).
Lời giải: Ta có y(-x) = cos(-x) + sin(-x) = cos(x) - sin(x). Vì y(-x) ≠ y(x) và y(-x) ≠ -y(x), nên hàm số y = cos(x) + sin(x) không chẵn, không lẻ.
Đề bài: Vẽ đồ thị hàm số y = sin(2x).
Lời giải: Đồ thị hàm số y = sin(2x) có chu kỳ T = π/2. Bảng giá trị:
| x | y |
|---|---|
| 0 | 0 |
| π/4 | 1 |
| π/2 | 0 |
| 3π/4 | -1 |
| π | 0 |
Vẽ đồ thị dựa trên bảng giá trị.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải bài 45 trang 109, 110 sách bài tập Toán 11 Cánh Diều. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!