Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 61 trang 119 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
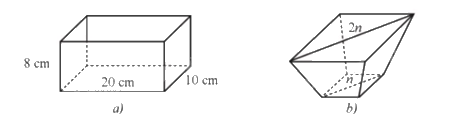
Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 20 cm
Đề bài
Một chiếc khay đựng đầy nước có dạng hình hộp chữ nhật với kích thước: chiều dài 20 cm, chiều rộng 10 cm, chiều cao 8 cm (hình vẽ a). Để san bớt nước cho đỡ đầy, người ta đổ nước từ chiếc khay thứ nhất đó sang chiếc khay thứ hai có dạng hình chóp cụt tứ giác đều với đáy khay là hình vuông nhỏ có đường chéo dài \(n\) (cm), miệng khay là hình vuông lớn có đường chéo dài \(2n\) (cm) (hình vẽ b). Sau khi đổ, mực nước ở khay thứ hai cao bằng \(\frac{2}{3}\) chiều cao của khay đó và lượng nước trong khay thứ nhất giảm đi \(\frac{1}{4}\) so với ban đầu. Tính thể tích của chiếc khay thứ hai theo đơn vị centimét khối.
Phương pháp giải - Xem chi tiết
Do khi đổ nước từ khay nước a sang khay nước b, ta thấy tổng thể tích nước ở hai khay không thay đổi, do đó ta có thể tính được lượng nước đã đổ sang khay b.
Do chiều cao mực nước của khay b cao bằng \(\frac{2}{3}\) chiều cao khay b, nên có thể coi “hình dạng” của nước trong khay b là một khối chóp cụt tứ giác đều, nên ta có thể gọi chiều cao của nước trong khay b là \(h\), và tính diện tích đáy còn lại của khối chóp này. Lúc này ta sẽ tính dược tích \({n^2}h\), từ đó có thể tính được thể tích của khay b.
Lời giải chi tiết
Ban đầu, thể tích nước có ở trong khay a là \(8.20.10 = 1600{\rm{ }}\left( {c{m^3}} \right)\).
Sau khi đổ nước sang khay thứ hai, ta thấy rằng lượng nước trong khay a giảm đi \(\frac{1}{4}\) so với ban đầu, cho nên ta suy ra lượng nước có ở trong khay b bằng \(\frac{1}{4}\) lượng nước ban đầu có ở trong khay a.
Thể tích nước trong khay b là \(1600.\frac{1}{4} = 400{\rm{ }}\left( {c{m^3}} \right)\).
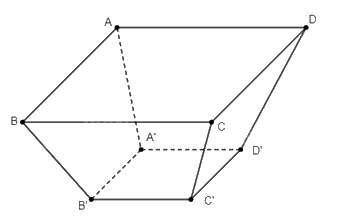
Giả sử khay b có hình dạng chóp cụt tứ giác đều \(ABCD.A'B'C'D'\) như hình vẽ dưới đây (với \(A'B'C'D'\) là đáy bé).
Xét hình thang cân \(ACC'A'\), gọi \(H\) và \(K\) lần lượt là hình chiếu của \(A'\) và \(C'\) trên \(AC\). Trên \(C'K\), lấy điểm \(P\) sao cho \(\frac{{C'P}}{{C'K}} = \frac{2}{3}\). Đường thẳng qua \(P\) và song song với \(AC\) cắt \(AA'\), \(A'H\), \(C'C\) lần lượt tại \(M\), \(N\) và \(Q\).
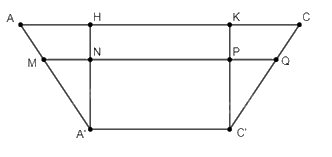
Do chiều cao mực nước trong khay b bằng \(\frac{2}{3}\) chiều cao khay, nên ta có thể coi \(C'P\) chính là chiều cao nước trong khay.
Gọi chiều cao của khay b là \(h{\rm{ }}\left( {cm} \right)\). Theo hình vẽ, ta thấy rằng \(A'H = C'K = h\). Suy ra \(C'P = \frac{2}{3}h\), có nghĩa chiều cao nước trong khay b là \(\frac{2}{3}h\).
Do \(AC = 2n\), \(A'C' = n\) và \(AH = CK\), nên ta suy ra \(AH = CK = \frac{n}{2}\) và \(HK = NP = n\).
Tam giác \(A'AH\) có \(MN\parallel AH\), nên theo định lí Thales, ta có:
\(\frac{{MN}}{{AH}} = \frac{{A'N}}{{AH}} = \frac{2}{3} \Rightarrow MN = \frac{2}{3}AH = \frac{n}{3}\)
Chứng minh tương tự ta cũng có \(PQ = \frac{n}{3}\). Do đó \(MQ = n + \frac{n}{3} + \frac{n}{3} = \frac{{5n}}{3}\).
Vậy nước trong khay b có dạng hình chóp cụt tứ giác đều, với hai đáy là các hình vuông có đường chéo lần lượt là \(n\) và \(\frac{{5n}}{3}\). Do đó, thể tích nước trong khay b là:
\(V = \frac{1}{3}\left( {\frac{2}{3}h} \right)\left( {\frac{{{n^2}}}{2} + \sqrt {\frac{{{n^2}}}{2}.\frac{{{{\left( {\frac{{5n}}{3}} \right)}^2}}}{2}} + \frac{{{{\left( {\frac{{5n}}{3}} \right)}^2}}}{2}} \right) = \frac{{49}}{{81}}{n^2}h\).
Mà thể tích nước trong khay là \(400{\rm{ }}c{m^3}\), nên ta có \(\frac{{49}}{{81}}{n^2}h = 400 \Rightarrow {n^2}h = \frac{{32400}}{{49}}\).
Vậy thể tích khay b là:
\(V = \frac{1}{3}h\left( {\frac{{{n^2}}}{2} + \sqrt {\frac{{{n^2}}}{2}.\frac{{{{\left( {2n} \right)}^2}}}{2}} + \frac{{{{\left( {2n} \right)}^2}}}{2}} \right) = \frac{7}{6}{n^2}h = \frac{7}{6}.\frac{{32400}}{{49}} = \frac{{5400}}{7}{\rm{ }}\left( {c{m^3}} \right)\).
Bài 61 trang 119 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ, và các tính chất hình học khác.
Bài 61 thường bao gồm các dạng bài tập sau:
Để giải bài 61 trang 119 sách bài tập Toán 11 - Cánh Diều, chúng ta cần nắm vững các kiến thức sau:
Dưới đây là ví dụ về lời giải một dạng bài tập thường gặp trong bài 61:
Cho hai vectơ a = (1; 2; -1) và b = (-2; 0; 3). Tính góc giữa hai vectơ a và b.
Lời giải:
Ta có: a.b = (1)(-2) + (2)(0) + (-1)(3) = -2 + 0 - 3 = -5
|a| = √(1² + 2² + (-1)²) = √6
|b| = √((-2)² + 0² + 3²) = √13
Áp dụng công thức tính cosin góc giữa hai vectơ:
cos(θ) = (a.b) / (|a||b|) = -5 / (√6 * √13) = -5 / √78 ≈ -0.563
θ = arccos(-0.563) ≈ 124.2°
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 11 - Cánh Diều và các nguồn tài liệu học tập khác.
Bài 61 trang 119 sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng kiến thức về tích vô hướng của hai vectơ. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, bạn sẽ tự tin chinh phục bài tập này.