Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 44 trang 104 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 44 trang 104 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(\left( {SAC} \right) \bot \left( {ABCD} \right)\).
Đề bài
Cho hình chóp \(S.ABCD\) có \(ABCD\) là hình chữ nhật, \(\left( {SAC} \right) \bot \left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(AD\), \(\left( {SBM} \right) \bot \left( {ABCD} \right)\). Giả sử \(SA = 5a\), \(AB = 3a\), \(AD = 4a\) và góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(\varphi \). Tính \(\cos \varphi \).
Phương pháp giải - Xem chi tiết
Gọi \(H\) là giao điểm của \(BM\) và \(AC\). Ta chứng minh \(SH \bot \left( {ABCD} \right)\), từ đó suy ra \(\varphi = \widehat {SAH}\).
Lời giải chi tiết
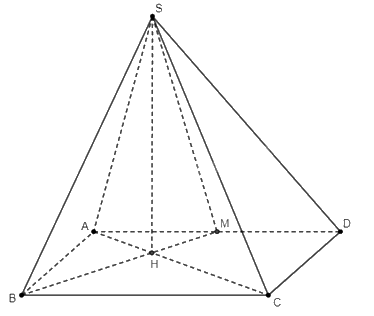
Gọi \(H\) là giao điểm của \(BM\) và \(AC\). Dễ dàng chứng minh được \(SH\) là giao tuyến của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBM} \right)\). Hơn nữa, do \(\left( {SAC} \right) \bot \left( {ABCD} \right)\) và \(\left( {SBM} \right) \bot \left( {ABCD} \right)\), ta suy ra \(SH \bot \left( {ABCD} \right)\), tức \(H\) là hình chiếu của \(S\) trên \(\left( {ABCD} \right)\).
Do đó góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABCD} \right)\) chính là góc \(\widehat {SAH}\), tức là \(\varphi = \widehat {SAH}\). Suy ra \(\cos \varphi = \cos \widehat {SAH} = \frac{{AH}}{{SA}}\).
Vì \(ABCD\) là hình chữ nhật, nên \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{\left( {3a} \right)}^2} + {{\left( {4a} \right)}^2}} = 5a\).
Ta có \(AM = \frac{1}{2}AD = \frac{1}{2}.4a = 2a\).
Do \(AM\parallel BC\), ta suy ra \(\frac{{AH}}{{HC}} = \frac{{AM}}{{BC}} = \frac{{2a}}{{4a}} = \frac{1}{2}\). Như vậy \(\frac{{AH}}{{AC}} = \frac{1}{3}\).
Suy ra \(AH = \frac{{AC}}{3} = \frac{{5a}}{3}\).
Do đó \(\cos \varphi = \frac{{AH}}{{SA}} = \frac{{\frac{{5a}}{3}}}{{5a}} = \frac{1}{3}\).
Bài 44 trang 104 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về phép biến hình. Bài tập này thường tập trung vào việc vận dụng các kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán hình học.
Bài 44 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 44 trang 104, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi. Lưu ý rằng, trước khi bắt đầu giải bài tập, bạn nên ôn lại lý thuyết về các phép biến hình và các công thức liên quan.
Câu hỏi: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến đó.
Lời giải:
Công thức phép tịnh tiến: A'(x'; y') = A(x; y) + v(a; b) = (x + a; y + b)
Áp dụng công thức vào bài toán:
A'(x'; y') = A(1; 2) + v(3; -1) = (1 + 3; 2 - 1) = (4; 1)
Vậy, ảnh A' của điểm A qua phép tịnh tiến theo vectơ v là A'(4; 1).
Ngoài sách giáo khoa và sách bài tập, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 11:
Hy vọng rằng, với những hướng dẫn chi tiết và hữu ích trên đây, bạn sẽ tự tin hơn trong việc giải bài 44 trang 104 sách bài tập Toán 11 Cánh Diều. Chúc bạn học tập tốt!