Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 74 trang 33 Sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm.
Đề bài
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách \(h\) (cm) từ chất điểm đến trục hoành được tính theo công thức \(h = \left| y \right|\), trong đó \(y = a\sin \left( {\frac{\pi }{5}t} \right)\), với \(t\) là thời gian chuyển động của chất điểm tính bằng giây \(\left( {t \ge 0} \right)\) và chất điểm bắt đầu chuyển động từ vị trí \(A\) (Xem hình dưới)
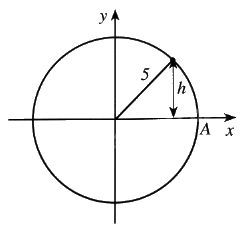
a) Chất điểm chuyển động một vòng hết bao nhiêu giây?
b) Tìm giá trị của \(a\).
c) Tìm thời điểm sao cho chất điểm ở vị trí có \(h = 2,5\) cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.
Phương pháp giải - Xem chi tiết
a) Thời gian chất điểm chuyển động một vòng là chu kì của chất điểm đó.
Xét \(h = 0 \Leftrightarrow y = 0 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = 0 \Leftrightarrow t = 5k\)\(\left( {k \in \mathbb{Z}} \right)\)
Nhận thấy \(k = 2\), ta thấy chất điểm và quay về vị trí\(A\). Do vậy, thời gian chất điểm chuyển động một vòng là 10 giây.
b) Do thời gian chất điểm chuyển động một vòng là 10 giây, nên sau 2,5 giây chất điểm chuyển động được một phần tư vòng tròn theo chiều dương. Như vậy tại \(t = 2,5\) ta có: \(a\sin \left( {\frac{\pi }{5}.\frac{5}{2}} \right) = 5 \Leftrightarrow a = 5\).
c) Yêu cầu đề bài tương đương với việc tìm \(t\) để \(y = 5\sin \left( {\frac{\pi }{5}t} \right) = - 2,5\).
Giải phương trình ẩn \(t\) và kết luận.
Lời giải chi tiết
a) Thời gian chất điểm chuyển động một vòng là chu kì của chất điểm đó.
Xét \(t = 0 \Rightarrow h = 0\), ta thấy chất điểm ở vị trí \(A\). Ta cần tìm thời gian gần nhất kể từ thời điểm \(t = 0\) (giây), chất điểm lại quay về vị trí \(A\).
Xét \(h = 0 \Leftrightarrow y = 0 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = 0 \Leftrightarrow t = 5k\)\(\left( {k \in \mathbb{Z}} \right)\)
Với \(k = 1\), ta thấy chất điểm chuyển động được nửa vòng tròn.
Với \(k = 2\), ta thấy chất điểm chuyển động được một vòng tròn, và quay về vị trí\(A\).
Do vậy, thời gian chất điểm chuyển động một vòng là 10 giây.
b) Do thời gian chất điểm chuyển động một vòng là 10 giây, nên sau 2,5 giây chất điểm chuyển động được một phần tư vòng tròn theo chiều dương. Như vậy tại \(t = 2,5\) ta có: \(y = \left| y \right| = h = 5 \Leftrightarrow a\sin \left( {\frac{\pi }{5}.\frac{5}{2}} \right) = 5 \Leftrightarrow a\sin \left( {\frac{\pi }{2}} \right) = 5 \Leftrightarrow a = 5\).
\( \Rightarrow y = 5\sin \left( {\frac{\pi }{5}t} \right)\)
c) Ta cần tìm \(t\) để \(h = 2,5\)cm và ở dưới trục hoành nên \(y = - 2,5\).
\(5\sin \left( {\frac{\pi }{5}t} \right) = - 2,5 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = - \frac{1}{2}\)
Ta thấy \(\sin \frac{{ - \pi }}{6} = - \frac{1}{2}\), phương trình ở trên tương đương với
\(\sin \left( {\frac{\pi }{5}t} \right) = \sin \frac{{ - \pi }}{6} \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{5}t = - \frac{\pi }{6} + k2\pi \\\frac{\pi }{5}t = \pi + \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = \frac{{ - 5 + 60k}}{6}\\t = \frac{{35 + 60k}}{6}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vì ta chỉ xét vòng quay đầu tiên, nên \(0 \le t \le 10\). Do đó \(t = \frac{{35}}{6}\), \(t = \frac{{55}}{6}\)
Vậy tại thời điểm \(t = \frac{{35}}{6}\) giây, \(t = \frac{{55}}{6}\) giây, chất điểm cách trục hoành 2,5 cm và nằm ở dưới trục hoành.
Bài 74 trang 33 Sách bài tập Toán 11 - Cánh Diều thuộc chương trình học Toán 11, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về đồ thị hàm số lượng giác, phương trình lượng giác và các tính chất của hàm số để giải quyết.
Trước khi bắt đầu giải bài tập, điều quan trọng nhất là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 74 trang 33, đề bài thường yêu cầu:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ cùng nhau đi qua từng bước giải một ví dụ cụ thể. Giả sử đề bài yêu cầu vẽ đồ thị hàm số y = sin(2x) và xác định tập giá trị của hàm số.
Ngoài dạng bài tập vẽ đồ thị hàm số, bài 74 trang 33 còn có thể xuất hiện các dạng bài tập khác như:
Để học tốt môn Toán 11, đặc biệt là chương Hàm số lượng giác, bạn nên:
Bài 74 trang 33 Sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về hàm số lượng giác. Hy vọng với hướng dẫn chi tiết và các lời khuyên trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!