Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 56 trang 117 sách bài tập Toán 11 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và phù hợp với chương trình học Toán 11 hiện hành.
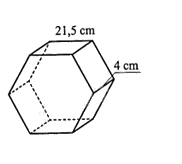
Người ta cần đổ bê tông để làm những viên gạch có dạng khối lăng trụ lục giác đều như hình bên với chiều cao là 4 cm
Đề bài
Người ta cần đổ bê tông để làm những viên gạch có dạng khối lăng trụ lục giác đều như hình bên với chiều cao là 4 cm và cạnh lục giác dài 21,5 cm. Tính thể tích bê tông theo đơn vị centimét khối để làm một viên gạch như thế (làm tròn kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Thể tích bê tông cần sử dụng để làm ra một viên gạch chính là thể thích khối lăng trụ lục giác đều. Công thức tính thể tích khối lăng trụ: \(V = Sh\), với \(S\) là diện tích đáy, \(h\) là chiều cao của khối lăng trụ.
Lời giải chi tiết
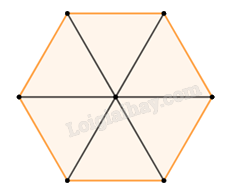
Nhận xét rằng đáy của viên gạch cần làm là lục giác đều. Ta chia lục giác đều nàyp bởi 6 tam giác đều cạnh 21,5 cm như hình vẽ. Do đó, diện tích đáy của viên gạch là \(S = 6.\frac{{21,{5^2}\sqrt 3 }}{4}\).
Vậy thể tích bê tông cần dùng để làm một viên gạch là
\(V = Sh = 6.\frac{{21,{5^2}\sqrt 3 }}{4}.4 \approx 4803,8{\rm{ }}\left( {c{m^3}} \right)\)
Bài 56 trang 117 sách bài tập Toán 11 - Cánh Diều thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Bài tập này thường tập trung vào việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, tính góc giữa đường thẳng và mặt phẳng, và giải các bài toán ứng dụng liên quan.
Bài 56 thường bao gồm các dạng bài tập sau:
Để giải bài tập 56 trang 117 sách bài tập Toán 11 - Cánh Diều hiệu quả, bạn cần nắm vững các kiến thức sau:
Bài 56: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Lời giải:
Ngoài bài 56, bạn có thể gặp các bài tập tương tự với các biến đổi nhỏ về dữ kiện hoặc yêu cầu. Để giải các bài tập này, bạn cần:
Để củng cố kiến thức và kỹ năng giải bài tập về đường thẳng và mặt phẳng trong không gian, bạn nên luyện tập thêm các bài tập khác trong sách bài tập Toán 11 - Cánh Diều và các tài liệu tham khảo khác.
Bài 56 trang 117 sách bài tập Toán 11 - Cánh Diều là một bài tập quan trọng giúp bạn hiểu sâu hơn về các khái niệm và phương pháp giải bài tập về đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, bạn sẽ tự tin hơn khi giải các bài tập tương tự.
| Khái niệm | Giải thích |
|---|---|
| Vectơ chỉ phương của đường thẳng | Vectơ song song với đường thẳng đó. |
| Vectơ pháp tuyến của mặt phẳng | Vectơ vuông góc với mặt phẳng đó. |
| Góc giữa đường thẳng và mặt phẳng | Góc giữa đường thẳng và hình chiếu của nó lên mặt phẳng. |