Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 44 trang 113 sách bài tập Toán 11 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 44 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.
Đề bài
Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.
Phương pháp giải - Xem chi tiết
Trước hết, cần chứng minh kết quả phụ: Trong một hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh của hình bình hành. Áp dụng kết quả này vào hình hộp.
Lời giải chi tiết
Trước hết, ta sẽ chứng minh kết quả phụ: Trong một hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh của hình bình hành. Xét hình bình hành \(MNPQ\) như hình dưới đây. Ta cần chứng minh rằng \(M{P^2} + N{Q^2} = M{N^2} + N{P^2} + P{Q^2} + Q{M^2}\)
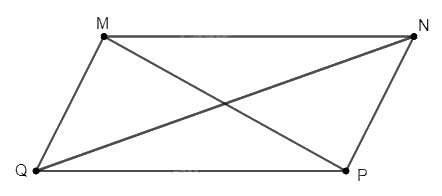
Áp dụng định lí cosin trong tam giác \(MPQ\) và \(NPQ\), ta có:
\(M{P^2} = Q{M^2} + Q{P^2} - 2QM.QP.\cos MQP\)
\(Q{N^2} = P{Q^2} + P{N^2} - 2PN.PQ.\cos QPN\).
Do \(QM = PN\) và \(\cos MQP = - \cos QPN\) (do \(\widehat {MQP}\) và \(\widehat {QPN}\) bù nhau), nên ta có
\(M{P^2} + N{Q^2} = M{Q^2} + 2P{Q^2} + P{N^2} - 2QM.QP\cos MQP + 2QM.QP\cos MQP\)
\( \Rightarrow M{P^2} + N{Q^2} = 2\left( {M{N^2} + N{P^2}} \right)\).
Ta có điều phải chứng minh.
Quay trở lại bài toán, ta xét hình hộp \(ABCD.A'B'C'D'\).
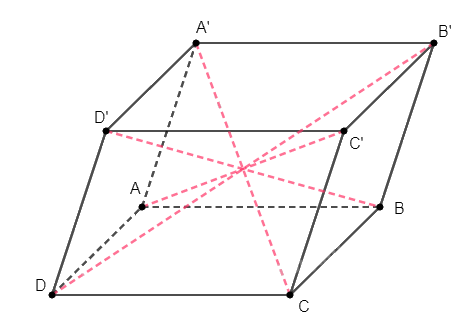
Áp dụng kết quả vừa chứng minh được ở trên với hai hình bình hành \(ACC'A'\), \(DBB'D'\) và \(A'B'C'D'\) ta có:
\(AC{'^2} + A'{C^2} = 2\left( {AA{'^2} + A'C{'^2}} \right)\) ; \(B'{D^2} + BD{'^2} = 2\left( {BB{'^2} + B'D{'^2}} \right)\);
\(A'C{'^2} + B'D{'^2} = 2\left( {A'B{'^2} + A'D{'^2}} \right)\).
Như vậy
\(AC{'^2} + A'{C^2} + BD{'^2} + B'{D^2} = 2\left( {AA{'^2} + A'C{'^2} + BB{'^2} + B'D{'^2}} \right)\)
\( = 4AA{'^2} + 2\left( {A'C{'^2} + B'D{'^2}} \right) = 4AA{'^2} + 4A'B{'^2} + 4A'D{'^2}\).
Do \(4AA{'^2} = AA{'^2} + BB{'^2} + CC{'^2} + DD{'^2}\), \(4A'B{'^2} = A'B{'^2} + A{B^2} + C'D{'^2} + C{D^2}\), \(4A'D{'^2} = A'D{'^2} + A{D^2} + B'C{'^2} + B{C^2}\), ta kết luận rằng trong một hình hộp, tổng bình phương tất cả các đường chéo bằng tổng tất cả các cạnh của hình hộp đó.
Bài toán được chứng minh.
Bài 44 trang 113 sách bài tập Toán 11 Cánh Diều thuộc chương trình học về phép biến hình. Bài tập này thường tập trung vào việc vận dụng các kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán hình học.
Bài 44 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài 44, chúng ta sẽ đi qua từng phần của bài tập. Dưới đây là lời giải chi tiết cho từng câu hỏi:
(Nêu lại đề bài câu a)
Lời giải:
(Giải thích chi tiết từng bước giải câu a, kèm theo hình vẽ minh họa nếu cần thiết. Sử dụng các công thức và định lý liên quan.)
(Nêu lại đề bài câu b)
Lời giải:
(Giải thích chi tiết từng bước giải câu b, kèm theo hình vẽ minh họa nếu cần thiết. Sử dụng các công thức và định lý liên quan.)
(Nêu lại đề bài câu c)
Lời giải:
(Giải thích chi tiết từng bước giải câu c, kèm theo hình vẽ minh họa nếu cần thiết. Sử dụng các công thức và định lý liên quan.)
Để giải quyết hiệu quả bài 44, bạn cần nắm vững các kiến thức sau:
Dưới đây là một số mẹo giúp bạn giải bài tập về phép biến hình một cách dễ dàng hơn:
Để củng cố kiến thức, bạn có thể làm thêm các bài tập tương tự sau:
Hy vọng với lời giải chi tiết và những kiến thức hữu ích trên, bạn đã có thể tự tin giải bài 44 trang 113 sách bài tập Toán 11 Cánh Diều. Chúc bạn học tập tốt!