Bài 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về giới hạn của hàm số. Bài tập này yêu cầu học sinh phải nắm vững định nghĩa về giới hạn và các tính chất của giới hạn để có thể giải quyết một cách chính xác.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau
Đề bài
Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau
a) \(\frac{\pi }{6}\);
b) \(\frac{{ - 5\pi }}{7}\);
c) \({270^0}\);
d) \( - {415^0}\).
Phương pháp giải - Xem chi tiết
Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \) là điểm M trên đường tròn lượng giác sao cho sđ(OA, OM) = \(\alpha \).
Lời giải chi tiết
a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\frac{\pi }{6}\) được xác định như trên hình.
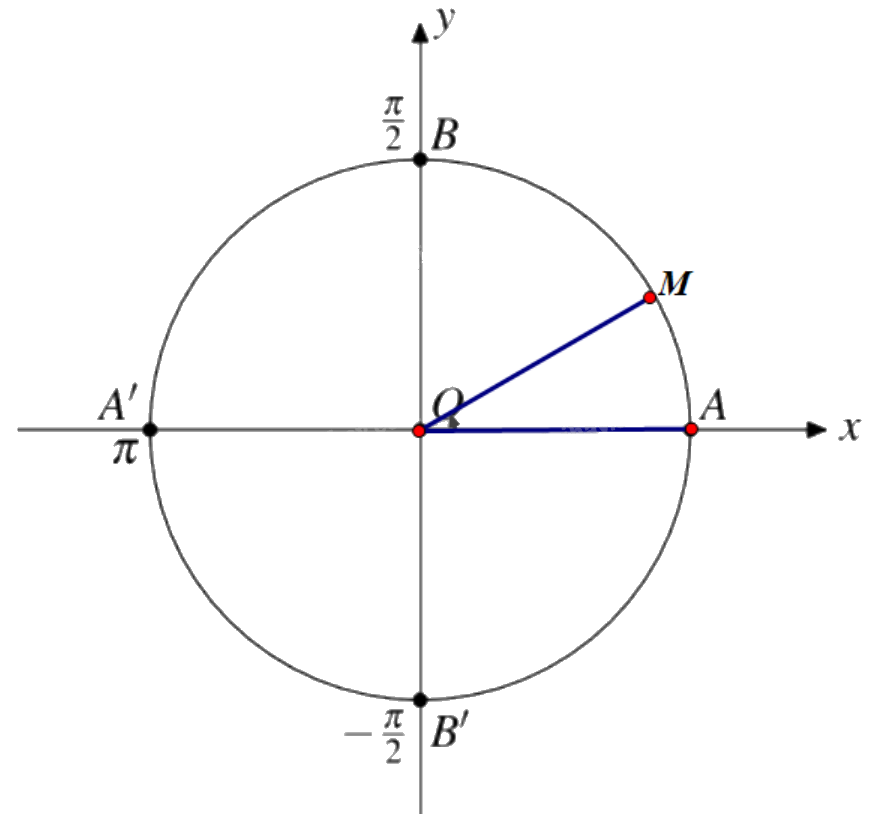
b) Điểm K trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\frac{{ - 5\pi }}{7}\) được xác định như trên hình.
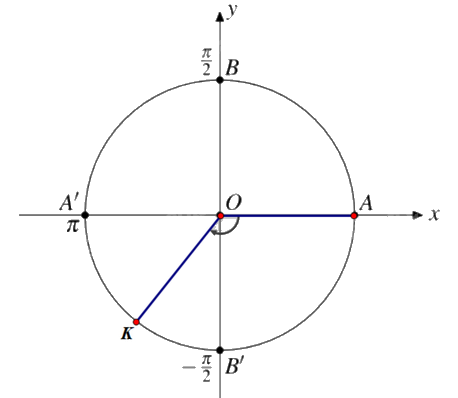
c) Điểm B’ trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \({270^0}\) được xác định như trên hình.
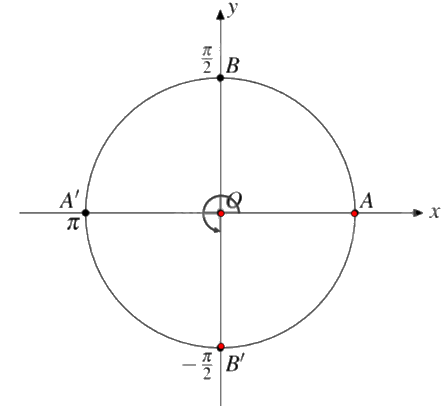
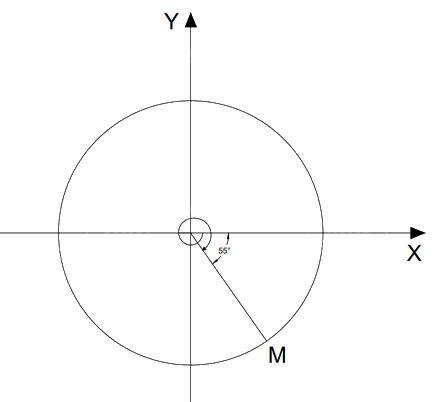
d) Để dễ dàng xác định góc hơn, ta tách \( - {415^0} = - {360^0} - {55^0}\).
Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \( - {415^0}\) được xác định như trên hình.
Bài 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức thuộc chương 1: Giới hạn. Đây là một trong những bài tập đầu tiên trong chương, giúp học sinh làm quen với khái niệm giới hạn của hàm số. Bài tập này thường yêu cầu học sinh tính giới hạn của hàm số tại một điểm hoặc khi x tiến tới vô cùng.
Bài tập 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức thường bao gồm các dạng bài sau:
Để giải bài tập 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức, học sinh cần nắm vững các kiến thức sau:
Dưới đây là lời giải chi tiết bài 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức:
Áp dụng định nghĩa giới hạn, ta có:
lim (2x + 1) khi x tiến tới 2 = 2 * 2 + 1 = 5
Ta có thể phân tích tử số thành (x - 2)(x + 2). Khi đó:
lim (x^2 - 4) / (x - 2) khi x tiến tới 2 = lim (x - 2)(x + 2) / (x - 2) khi x tiến tới 2 = lim (x + 2) khi x tiến tới 2 = 2 + 2 = 4
Ta biết rằng lim (1/x) khi x tiến tới vô cùng bằng 0.
Kiến thức về giới hạn có ứng dụng rất lớn trong toán học, đặc biệt là trong các lĩnh vực như:
Bài 1.2 trang 7 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức về giới hạn của hàm số. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và các bài tập tương tự.