Bài 4.37 trang 68 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng của đạo hàm để khảo sát hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.37, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, cập nhật và hữu ích nhất cho quá trình học tập của các bạn.
Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’
Đề bài
Cho ba mặt phẳng (P), (Q), (R) đôi một song song. Hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’. Biết rằng AB = 2cm, BC = 6cm và A’B’ = 3cm, tính B’C’.
Phương pháp giải - Xem chi tiết
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ
Lời giải chi tiết
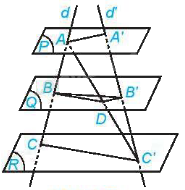
Vì ba mặt phẳng (P), (Q), (R) đôi một song song và hai đường thẳng d, d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ nên \(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) (định lí Thalès)\( \Rightarrow \frac{2}{6} = \frac{3}{{B'C'}} \Rightarrow B'C' = \frac{{3.6}}{2} = 9\left( {cm} \right)\)
Bài 4.37 trang 68 sách bài tập Toán 11 - Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để khảo sát hàm số bậc ba. Cụ thể, bài toán thường yêu cầu xác định khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số. Việc nắm vững các bước khảo sát hàm số bằng đạo hàm là chìa khóa để giải quyết bài toán này một cách hiệu quả.
Trước khi bắt đầu giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu. Thông thường, đề bài sẽ cho một hàm số bậc ba và yêu cầu khảo sát hàm số đó. Phương pháp giải bài này bao gồm các bước sau:
Để minh họa, chúng ta sẽ cùng giải một bài toán cụ thể. Giả sử hàm số cần khảo sát là: f(x) = x3 - 3x2 + 2
Tập xác định của hàm số là D = ℝ.
f'(x) = 3x2 - 6x
Giải phương trình f'(x) = 0, ta được: 3x2 - 6x = 0 => x = 0 hoặc x = 2
f''(x) = 6x - 6
Giải phương trình f''(x) = 0, ta được: 6x - 6 = 0 => x = 1
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số f(x) = x3 - 3x2 + 2. Đồ thị hàm số có điểm cực đại tại x = 0, điểm cực tiểu tại x = 2 và điểm uốn tại x = 1.
Việc khảo sát hàm số có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 4.37 trang 68 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng của đạo hàm để khảo sát hàm số. Hy vọng với lời giải chi tiết và các lưu ý trên, các em học sinh sẽ tự tin giải quyết bài toán này và các bài tập tương tự.