Bài 4.54 trang 72 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tích vô hướng, tính chất của vectơ để giải quyết các bài toán liên quan đến hình học phẳng.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.54 trang 72, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình hộp chữ nhật ABCD.A’B’C’D’
Đề bài
Cho hình hộp chữ nhật ABCD.A’B’C’D’. Hình chiếu song song của điểm A trên mặt phẳng (CDD’C’) theo phương BC’ là:
A. D’
B. D
C. B
D. C’
Phương pháp giải - Xem chi tiết
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
+ Nếu M thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
+ Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
Điểm M’ được gọi là hình chiếu của M trên mặt phẳng \(\left( \alpha \right)\) theo phương chiếu \(\Delta \).
Lời giải chi tiết
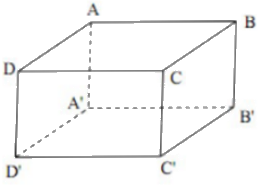
Đáp án A.
Tứ giác AD’C’B có: AB//D’C’ (cùng song song với A’B’), \(AB = C'D'\left( { = A'B'} \right)\) nên tứ giác AD’C’B là hình bình hành, do đó AD’//BC’.
Ta có, D’ là giao điểm của AD’ và mặt phẳng (CDD’C’), AD’//BC’.
Do đó, hình chiếu song song của điểm A trên mặt phẳng (CDD’C’) theo phương BC’ là điểm D’
Bài 4.54 trang 72 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán đòi hỏi học sinh phải nắm vững kiến thức về vectơ, đặc biệt là các khái niệm về tích vô hướng, hình chiếu của một vectơ lên một vectơ khác, và các tính chất liên quan. Để giải bài toán này một cách hiệu quả, chúng ta cần phân tích kỹ đề bài, xác định các vectơ liên quan, và áp dụng các công thức, định lý phù hợp.
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu. Thông thường, bài toán sẽ yêu cầu chúng ta tính một đại lượng nào đó liên quan đến vectơ, chẳng hạn như độ dài của một vectơ, góc giữa hai vectơ, hoặc diện tích của một hình. Đề bài cũng có thể yêu cầu chúng ta chứng minh một đẳng thức vectơ hoặc một tính chất hình học.
Tích vô hướng của hai vectơ a và b được định nghĩa là a.b = |a||b|cos(θ), trong đó θ là góc giữa hai vectơ. Tích vô hướng có nhiều ứng dụng quan trọng trong hình học, chẳng hạn như tính độ dài của một vectơ, tính góc giữa hai vectơ, và kiểm tra tính vuông góc của hai vectơ.
Hình chiếu của vectơ a lên vectơ b là một vectơ a' sao cho a' cùng phương với b và có độ dài bằng |a|cos(θ), trong đó θ là góc giữa hai vectơ a và b. Hình chiếu của một vectơ lên một vectơ khác có thể được sử dụng để giải quyết nhiều bài toán hình học.
Giả sử đề bài yêu cầu tính độ dài của cạnh huyền trong một tam giác vuông, biết độ dài hai cạnh góc vuông. Chúng ta có thể sử dụng định lý Pitago để giải bài toán này. Tuy nhiên, nếu chúng ta muốn sử dụng kiến thức về vectơ, chúng ta có thể biểu diễn các cạnh của tam giác vuông dưới dạng các vectơ và sử dụng tích vô hướng để tính độ dài của cạnh huyền.
Bài 4.54 trang 72 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bằng cách nắm vững kiến thức về tích vô hướng, hình chiếu của một vectơ lên một vectơ khác, và các tính chất liên quan, học sinh có thể giải quyết bài toán này một cách hiệu quả. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.
| Công thức | Mô tả |
|---|---|
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ |
| |a| = √(x2 + y2) | Độ dài của vectơ a |
| cos(θ) = (a.b) / (|a||b|) | Góc giữa hai vectơ |