Bài 4.52 trang 72 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp cận nhất, giúp các em học sinh tự tin hơn trong quá trình học tập môn Toán.
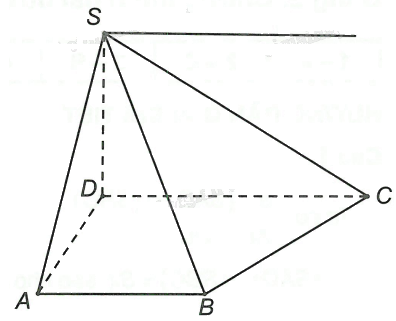
Chọn hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD).
Đề bài
Chọn hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Khi đó, d đi qua S và song song với
A. AC
B. CD
C. BD
D. BC
Phương pháp giải - Xem chi tiết
Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết
Đáp án B.
Vì AB//CD, CD nằm trong mặt phẳng (SCD) và S là giao điểm của hai mặt phẳng (SAB) và (SCD).
Do đó, giao tuyến d là đường thẳng d qua S và song song với CD.
Bài 4.52 yêu cầu chúng ta giải quyết một bài toán liên quan đến vectơ trong không gian. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Phân tích bài toán:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, bài toán sẽ cung cấp thông tin về các điểm trong không gian và yêu cầu tính toán các đại lượng liên quan đến vectơ, chẳng hạn như độ dài vectơ, góc giữa hai vectơ, hoặc kiểm tra xem hai vectơ có vuông góc hay không.
Lời giải chi tiết:
Để giải bài 4.52 trang 72 sách bài tập Toán 11 - Kết nối tri thức, chúng ta sẽ thực hiện theo các bước sau:
Ví dụ minh họa:
Giả sử đề bài yêu cầu tính góc giữa hai vectơ a = (1, 2, 3) và b = (-1, 0, 1). Chúng ta sẽ thực hiện như sau:
1. Tính tích vô hướng của hai vectơ:
a ⋅ b = (1)(-1) + (2)(0) + (3)(1) = -1 + 0 + 3 = 2
2. Tính độ dài của mỗi vectơ:
|a| = √(1² + 2² + 3²) = √14
|b| = √((-1)² + 0² + 1²) = √2
3. Tính góc giữa hai vectơ:
cos θ = (a ⋅ b) / (|a| |b|) = 2 / (√14 √2) = 2 / √28 = 2 / (2√7) = 1/√7
θ = arccos(1/√7) ≈ 69.3°
Lưu ý quan trọng:
Trong quá trình giải bài toán, cần chú ý đến việc sử dụng đúng các công thức và đơn vị đo. Ngoài ra, việc vẽ hình minh họa có thể giúp chúng ta hiểu rõ hơn về bài toán và tìm ra lời giải chính xác.
Mở rộng kiến thức:
Để nâng cao kiến thức về vectơ, các em có thể tìm hiểu thêm về các ứng dụng của vectơ trong các lĩnh vực khác nhau, chẳng hạn như vật lý, kỹ thuật, và khoa học máy tính. Việc nắm vững kiến thức về vectơ sẽ giúp các em giải quyết các bài toán phức tạp hơn một cách dễ dàng.
Bài tập tương tự:
Để rèn luyện kỹ năng giải bài toán về vectơ, các em có thể tự giải các bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Kết luận:
Bài 4.52 trang 72 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn trong quá trình học tập môn Toán.