Bài 4.46 trang 71 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.46 trang 71, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong các hình sau, hình nào là hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang?
Đề bài
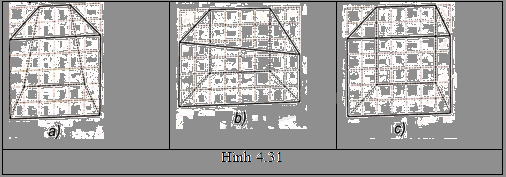
Trong các hình sau, hình nào là hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang?
Phương pháp giải - Xem chi tiết
Quan sát hình 4.31 để trả lời.
Lăng trụ tứ giác có hai đáy là hình thang, các mặt bên là hình bình hành.
Lời giải chi tiết
Hình biểu diễn của lăng trụ tứ giác có hai đáy là hình thang là hình 4.31c.
Bài 4.46 trang 71 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Dưới đây là lời giải chi tiết bài 4.46 trang 71 sách bài tập Toán 11 - Kết nối tri thức:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Bước 1: Xác định các yếu tố cần thiết
Để tính góc giữa đường thẳng SC và mặt phẳng (ABCD), ta cần xác định hình chiếu của điểm S lên mặt phẳng (ABCD). Vì SA vuông góc với (ABCD) nên A là hình chiếu của S lên (ABCD).
Bước 2: Tính độ dài các cạnh
Ta có: AC = a√2 (đường chéo hình vuông)
SC = √(SA² + AC²) = √(a² + (a√2)²) = √(a² + 2a²) = a√3
Bước 3: Tính góc giữa SC và mặt phẳng (ABCD)
Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Ta có:
tan α = SA / AC = a / (a√2) = 1/√2
α = arctan(1/√2) ≈ 35.26°
Kết luận: Góc giữa đường thẳng SC và mặt phẳng (ABCD) là khoảng 35.26°.
Bài tập này yêu cầu học sinh vận dụng kiến thức về hình học không gian, đặc biệt là các khái niệm về góc giữa đường thẳng và mặt phẳng. Để giải bài tập này một cách hiệu quả, học sinh cần:
Ngoài ra, học sinh có thể tham khảo thêm các bài tập tương tự để rèn luyện kỹ năng giải toán. Việc luyện tập thường xuyên sẽ giúp học sinh nắm vững kiến thức và tự tin hơn khi làm bài kiểm tra.
Các bài tập liên quan đến góc giữa đường thẳng và mặt phẳng thường yêu cầu học sinh tính góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng. Để giải các bài tập này, học sinh cần:
Ví dụ:
Hy vọng với lời giải chi tiết và phân tích trên, các em học sinh đã hiểu rõ cách giải bài 4.46 trang 71 sách bài tập Toán 11 - Kết nối tri thức. Chúc các em học tập tốt!
Lưu ý: Đây chỉ là một ví dụ về lời giải. Học sinh có thể tìm hiểu thêm các phương pháp giải khác để hiểu sâu hơn về bài toán.