Bài 1.34 trang 25 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.34 trang 25 Sách bài tập Toán 11 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho \(\frac{\pi }{2} < \alpha < \pi \). Mệnh đề nào sau đây đúng?
Đề bài
Cho \(\frac{\pi }{2} < \alpha < \pi \). Mệnh đề nào sau đây đúng?
A. \(\sin \alpha < 0;\,\,\cos \alpha > 0\).
B. \(\sin \alpha > 0;\,\,\cos \alpha > 0\).
C. \(\sin \alpha < 0;\,\,\cos \alpha < 0\).
D. \(\sin \alpha > 0;\,\,\cos \alpha < 0\).
Phương pháp giải - Xem chi tiết
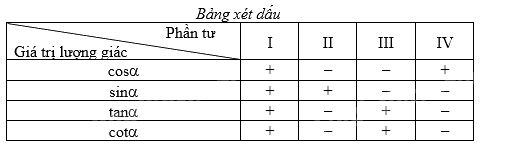
Dựa vào bảng dấu của góc lượng giác, ta chọn đáp án đúng
Lời giải chi tiết
Đáp án D.
Do \(\frac{\pi }{2} < \alpha < \pi \). Nên góc \(\alpha \) thuộc góc phần tư thứ II
Vì thế đáp án đúng là: \(\sin \alpha > 0;\,\,\cos \alpha < 0\).
Bài 1.34 trang 25 Sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 1.34 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 1.34, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể. Giả sử bài tập yêu cầu:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
Lời giải:
Vậy, góc giữa đường thẳng SB và mặt phẳng (ABCD) là 45°.
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với lời giải chi tiết, giúp các em tự tin hơn trong kỳ thi.
Bài 1.34 trang 25 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về vectơ. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!