Bài 4.35 trang 68 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.35 này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và hữu ích nhất để hỗ trợ quá trình học tập của các bạn.
Cho hình hộp ABCD.A’B’C’D’.
Đề bài
Cho hình hộp ABCD.A’B’C’D’.
a) Xác định giao tuyến d của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Chứng minh rằng d // AD.
c) Chứng minh rằng d đi qua trung điểm của các đường chéo của hình hộp.
Phương pháp giải - Xem chi tiết
Đường thẳng chung d (nếu có) của hai mặt phẳng phân biệt (P) và (Q) được gọi là giao tuyến của hai mặt phẳng đó.
Lời giải chi tiết
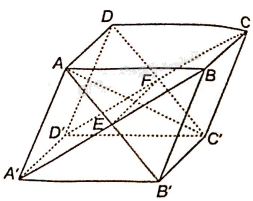
a) Gọi E là giao điểm của AB’ và A’B; gọi F là giao điểm của CD’ và C’D. Vì đường thẳng EF vừa thuộc cả hai mặt phẳng (ADC’B’) và (A’D’CB) nên EF là giao tuyến của hai mặt phẳng (ADC’B’) và (A’D’CB).
b) Hai mặt phẳng (ADC’B’) và (A’D’CB) chứa hai đường thẳng song song là AD và BC nên giao tuyến EF của hai mặt phẳng đó song song với AD.
c) Tứ giác ABCD và BCC’B’ là hình bình hành nên AD//BC, \(AD = BC\) và BC//B’C’ và \(BC = B'C'\), do đó ADC’B’ là hình bình hành.
Vì E, F lần lượt là trung điểm của AB’ và CD’ nên EF đi qua trung điểm của AC’. Vì các đường chéo của hình hộp cùng đi qua trung điểm của mỗi đường nên đường thẳng EF đi qua trung điểm các đường chéo đó.
Bài 4.35 trang 68 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán liên quan đến hình học. Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng đi vào phân tích chi tiết:
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC, tìm tập hợp các điểm M sao cho...)
Để giải bài 4.35, chúng ta cần thực hiện các bước sau:
Giả sử đề bài yêu cầu tìm tập hợp các điểm M sao cho MA + MB = 0. Trong trường hợp này, ta có thể sử dụng quy tắc trung điểm của đoạn thẳng để suy ra M là trung điểm của đoạn AB.
Để củng cố kiến thức về vectơ và ứng dụng trong hình học, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức.
Bài 4.35 trang 68 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Bằng cách phân tích đề bài, sử dụng kiến thức về vectơ và thực hiện các bước giải một cách cẩn thận, bạn có thể tự tin giải quyết bài tập này và các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng vectơ |
| (a + b) + c = a + (b + c) | Tính kết hợp của phép cộng vectơ |
| a.b = |a||b|cos(θ) | Công thức tính tích vô hướng của hai vectơ |
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ hiểu rõ hơn về cách giải bài 4.35 trang 68 sách bài tập Toán 11 Kết nối tri thức. Chúc các bạn học tập tốt!