Bài 1.23 trang 18 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.23 trang 18 Sách bài tập Toán 11 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
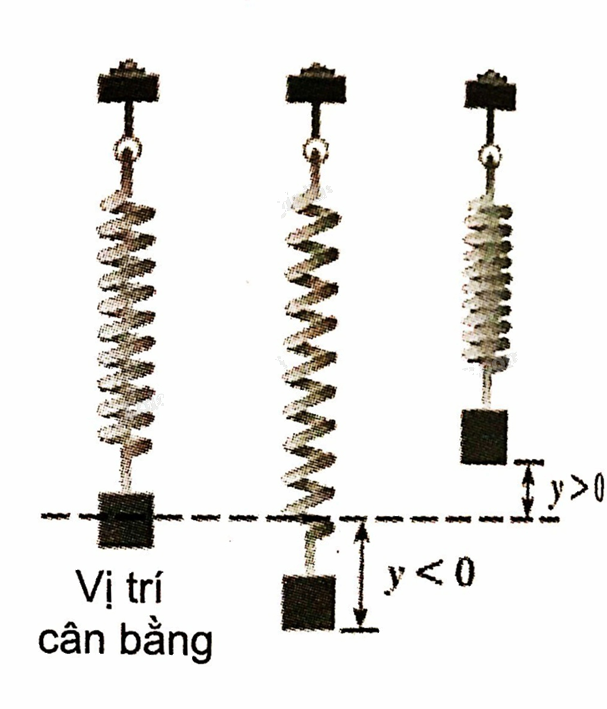
Một con lắc lò xo dạo động điều hòa quanh vị trí cân bằng theo phương trình ở đó \(y = 25\sin 4\pi t\), y được tính bằng centimet còn thời gian t được tính bằng giây.
Đề bài
Một con lắc lò xo dạo động điều hòa quanh vị trí cân bằng theo phương trình
ở đó \(y = 25\sin 4\pi t\), y được tính bằng centimet còn thời gian t được tính bằng giây.
a) Tìm chu kì dao động của con lắc lò xo.
b) Tìm tần số dao động của con lắc, tức là số lần dao động trong một giây.
c) Tìm khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc.
Phương pháp giải - Xem chi tiết
Chu kì dao động của hàm y = A.sin \(\omega \)x tìm dựa vào công thức \(T = \frac{{2\pi }}{\omega }\).
Tìm được chu kì, ta sẽ tìm được số dao động của con lắc trong 1 giây (tức tần số dao động).
Khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc chính là 2 lần biên độ dao động A.
Lời giải chi tiết
a) Hàm số \(y = 25\sin 4\pi t\) tuần hoàn với chu kì \(T = \frac{{2\pi }}{{4\pi }} = \frac{1}{2}\). Suy ra chu kì dao động của con lắc lò xo (tức là khoảng thời gian để con lắc thực hiện được một dao động toàn phần) là \(T = \frac{1}{2}\) (giây).
b) Vì chu kì dao động của con lắc là \(T = \frac{1}{2}\) (giây) nên trong 1 giây con lắc thực hiện được 2 dao động, tức là tần số dao động của con lắc là \(f = \frac{1}{T} = 2\,{\rm{Hz}}\).
c) Vì phương trình dao động của con lắc là \(y = 25\sin 4\pi t\), nên biên độ dao động của nó là A=25cm. Từ đó, khoảng cách giữa điểm cao nhất và điểm thấp nhất của con lắc là 2A=50cm.
Bài 1.23 trang 18 Sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 1.23 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 1.23 trang 18, chúng ta sẽ đi vào phân tích từng bước cụ thể. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng, và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Giả sử bài tập yêu cầu chứng minh rằng A, B, C thẳng hàng. Ta có thể sử dụng phương pháp chứng minh vectơ AB và AC cùng phương. Cụ thể:
Sau khi nắm vững cách giải bài 1.23, các em có thể tự luyện tập với các bài tập tương tự để củng cố kiến thức. Một số bài tập gợi ý:
Để giải bài tập về vectơ một cách hiệu quả, các em cần lưu ý những điều sau:
Bài 1.23 trang 18 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể của Giaitoan.edu.vn, các em sẽ tự tin hơn khi đối mặt với bài tập này và các bài tập tương tự trong tương lai.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |