Bài 4.47 trang 71 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.47 trang 71, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
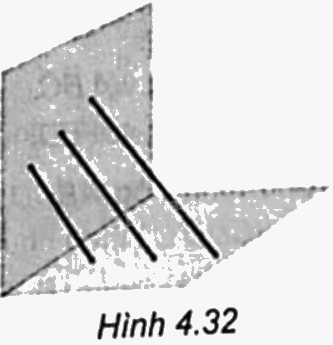
Ba chiếc gậy được đặt dựa vào tường và đôi một song song với nhau (H.4.32).
Đề bài
Ba chiếc gậy được đặt dựa vào tường và đôi một song song với nhau (H.4.32). Giải thích vì sao nếu ba đầu gậy trên tường thẳng hàng thì ba đầu gậy trên sàn cũng thẳng hàng.
Phương pháp giải - Xem chi tiết
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Lời giải chi tiết
Gọi d là đường thẳng song song với ba chiếc gậy và (P) là mặt sàn. Khi đó ba đầu gậy trên sàn chính là hình chiếu của ba đầu gậy trên tường qua phép chiếu lên mặt phẳng (P) theo phương d. Vì phép chiếu song song bảo toàn tính thẳng thàng của các điểm nên nếu ba đầu gậy trên tường thì ba đầu gậy trên sàn cũng thẳng hàng.
Bài 4.47 trang 71 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Để giải bài toán này, chúng ta cần nắm vững các kiến thức cơ bản về:
Đề bài: (Giả sử đề bài cụ thể của bài 4.47 được đưa ra ở đây. Ví dụ: Cho hình chóp S.ABCD, đáy là hình vuông cạnh a, SA vuông góc với đáy và SA = a. Gọi M là trung điểm của CD. Chứng minh rằng SM vuông góc với mặt phẳng (ABCD).)
Để giải bài toán này, chúng ta thực hiện các bước sau:
Ví dụ lời giải cho đề bài giả định:
Ta có: SA vuông góc với (ABCD) (theo giả thiết). Mà M là trung điểm của CD nên M thuộc (ABCD). Do đó, SA vuông góc với SM.
Xét tam giác SAM vuông tại A, ta có: SM2 = SA2 + AM2 = a2 + (a/2)2 = (5/4)a2. Suy ra SM = (a√5)/2.
Xét tam giác MCD, ta có: MC = MD = a/2. Do đó, tam giác MCD cân tại M.
Vì SA vuông góc với (ABCD) nên SA vuông góc với CD. Mà M là trung điểm của CD nên AM vuông góc với CD.
Do đó, CD vuông góc với (SAM). Suy ra CD vuông góc với SM.
Vậy, SM vuông góc với CD và SM vuông góc với SA. Do đó, SM vuông góc với mặt phẳng (ABCD).
Để củng cố kiến thức về vị trí tương đối giữa đường thẳng và mặt phẳng, các em có thể tham khảo các bài tập tương tự sau:
Bài 4.47 trang 71 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ về vị trí tương đối giữa đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!