Bài 7.49 trang 42 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay sau đây!
Cho hình lập phương ABCD.A’B’C’D’ thể tích khối tứ diện ABC’D’ bằng
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ thể tích khối tứ diện ABC’D’ bằng
A. \(\frac{{{a^3}}}{3}\).
B. \(\frac{{{a^3}}}{2}\).
C. \(\frac{{{a^3}}}{6}\).
D. \(\frac{{2{a^3}}}{3}\).
Phương pháp giải - Xem chi tiết
Cách 1: Tính thể tích phần bù
Ta có \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - \left( {{V_{B'.ABC}} + {V_{C.B'C'D'}} + {V_{D'.ACD}} + {V_{A.A'B'D'}}} \right)\).
Mà \({V_{ABCD.A'B'C'D'}} = {a^3}\) và \({V_{B'.ABC}} = {V_{C.B'C'D'}} = {V_{D'.ACD}} = {V_{A.A'B'D'}} = \frac{1}{3}.A'A.{S_{A'B'D'}} = \frac{1}{3}.a.\frac{1}{2}{a^2} = \frac{1}{6}{a^3}\).
\( \Rightarrow {V_{ACB'D'}} = \)
Cách 2: Sử dụng công thức \({V_{ACB'D'}} = \frac{1}{6}AC.B'D'.d\left( {AC,B'D'} \right).\sin \left( {AC,B'D'} \right)\)
Lời giải chi tiết
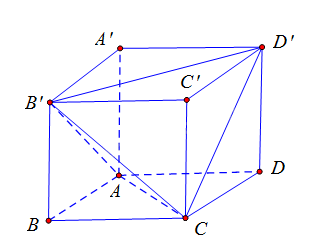
Cách 1:
Ta có \({V_{ACB'D'}} = {V_{ABCD.A'B'C'D'}} - \left( {{V_{B'.ABC}} + {V_{C.B'C'D'}} + {V_{D'.ACD}} + {V_{A.A'B'D'}}} \right)\).
Mà \({V_{ABCD.A'B'C'D'}} = {a^3}\) và \({V_{B'.ABC}} = {V_{C.B'C'D'}} = {V_{D'.ACD}} = {V_{A.A'B'D'}} = \frac{1}{3}.A'A.{S_{A'B'D'}} = \frac{1}{3}.a.\frac{1}{2}{a^2} = \frac{1}{6}{a^3}\).
Do đó \({V_{ACB'D'}} = {a^3} - \frac{4}{6}{a^3} = \frac{{{a^3}}}{3}\).
Cách 2: Sử dụng công thức \({V_{ACB'D'}} = \frac{1}{6}AC.B'D'.d\left( {AC,B'D'} \right).\sin \left( {AC,B'D'} \right)\)
\({V_{ACB'D'}} = \frac{1}{6}a\sqrt 2 .a\sqrt 2 .a.\sin {90^ \circ } = \frac{{{a^3}}}{3}\)
Bài 7.49 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết một bài toán hình học cụ thể. Bài toán thường liên quan đến việc chứng minh đẳng thức vectơ, tìm tọa độ điểm, hoặc xác định mối quan hệ giữa các điểm trong mặt phẳng tọa độ.
Để giải bài 7.49 trang 42 hiệu quả, trước tiên cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lựa chọn phương pháp giải phù hợp, thường là sử dụng các tính chất của vectơ, các công thức liên quan đến tọa độ vectơ, và các định lý hình học đã học.
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng, và sử dụng các ký hiệu toán học chính xác. Ví dụ:)
Để giúp các em hiểu rõ hơn về cách giải bài 7.49, chúng ta cùng xét một ví dụ minh họa cụ thể:
(Ví dụ minh họa với một bài toán tương tự, có lời giải chi tiết.)
Ngoài bài 7.49, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. Dưới đây là một số dạng bài tập thường gặp và cách giải:
Để giải các bài tập về vectơ nhanh chóng và chính xác, các em có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, các em nên luyện tập thêm với các bài tập khác trong sách bài tập và các đề thi thử. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập khác với mức độ khó tăng dần.
Bài 7.49 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và ứng dụng trong hình học. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin giải quyết bài toán này và các bài tập tương tự một cách hiệu quả.
| Công thức | Mô tả |
|---|---|
| AB = B - A | Vectơ AB được tính bằng hiệu tọa độ của điểm B và điểm A. |
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ a và b. |
| a x b = |a||b|sin(θ) | Tích có hướng của hai vectơ a và b. |