Bài 7.30 trang 38 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập này.
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = a,AD = a\sqrt 2 ,AA' = a\sqrt 3 \). Tính theo a khoảng cách:
Đề bài
Cho hình hộp chữ nhật \(ABCD \cdot A'B'C'D'\) có \(AB = a,AD = a\sqrt 2 ,AA' = a\sqrt 3 \). Tính theo a khoảng cách:
a) Từ điểm \(A\) đến mặt phẳng \(\left( {BDD'B'} \right)\).
b) Giữa hai đường thẳng \(BD\) và \(CD'\).
Phương pháp giải - Xem chi tiết
a) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {BDD'B'} \right)\).
Bước 1: Tìm hình chiếu vuông góc của \(A\) xuống mặt phẳng \(\left( {BDD'B'} \right)\).
Ta có \(\left( {ABCD} \right) \bot \left( {BB'D'D} \right)\).
Kẻ \(AH\) vuông góc với \(BD\) tại \(H\).
Khi đó \(AH \bot \left( {BB'D'D} \right)\), suy ra \(d\left( {A,\left( {BB'D'D} \right)} \right) = AH\)
Bước 2: Tính \(AH\)
b) Tính khoảng cách giữa hai đường thẳng \(BD\) và \(CD'\).
Bước 1: Dựng mặt phẳng qua đường thẳng \(BD\) và song song với \(CD'\) là \(\left( {A'BD} \right)\)
Chuyển khoảng cách về chân đường vuông góc\(d\left( {CD',BD} \right) = d\left( {CD',\left( {A'BD} \right)} \right) = d\left( {C,\left( {A'BD} \right)} \right) = d\left( {A,\left( {A'BD} \right)} \right){\rm{.\;}}\)
Bước 2: Tính \(d\left( {A,\left( {A'BD} \right)} \right) \Rightarrow \)\(d\left( {CD',BD} \right)\).
Lời giải chi tiết
a) Kẻ \(AH\) vuông góc với \(BD\) tại \(H\). Khi đó \(AH \bot \left( {BB'D'D} \right)\), suy ra
\(d\left( {A,\left( {BB'D'D} \right)} \right) = AH = \frac{{AB \cdot AD}}{{BD}} = \frac{{a\sqrt 6 }}{3}\).
b) Ta có: \(CD'//\left( {A'BD} \right)\) nên\(d\left( {CD',BD} \right) = d\left( {CD',\left( {A'BD} \right)} \right) = d\left( {C,\left( {A'BD} \right)} \right){\rm{.\;}}\)
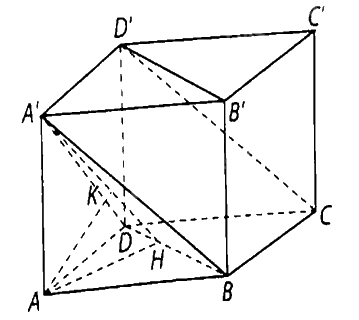
Vì \(AC\) cắt \(BD\) tại trung điểm của \(AC\) nên \(d\left( {C,\left( {A'BD} \right)} \right) = d\left( {A,\left( {A'BD} \right)} \right)\).
Kẻ \(AK\) vuông góc với \(A'H\) tại \(K\).
Khi đó \(AK \bot \left( {A'BD} \right)\), suy ra \(d\left( {A,\left( {A'BD} \right)} \right) = AK = \frac{{AH \cdot AA'}}{{A'H}} = \frac{{a\sqrt {66} }}{{11}}\). Vậy \(d\left( {CD',BD} \right) = \frac{{a\sqrt {66} }}{{11}}\).
Bài 7.30 trang 38 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về đạo hàm và cách sử dụng đạo hàm để giải quyết các vấn đề liên quan đến tốc độ thay đổi của một đại lượng.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ các yếu tố quan trọng: đại lượng cần tìm, các điều kiện cho trước và mối quan hệ giữa các đại lượng đó. Việc phân tích đề bài một cách cẩn thận sẽ giúp chúng ta xây dựng phương án giải quyết bài toán một cách hiệu quả.
Để giải bài 7.30 trang 38, chúng ta sẽ sử dụng phương pháp đạo hàm để tìm ra mối quan hệ giữa các đại lượng và từ đó giải quyết bài toán. Cụ thể, chúng ta sẽ thực hiện các bước sau:
Dưới đây là lời giải chi tiết cho bài 7.30 trang 38 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống:
(Giải bài tập cụ thể tại đây - ví dụ minh họa, cần thay thế bằng lời giải chính xác)
Ví dụ, giả sử bài toán yêu cầu tìm vận tốc của một vật tại thời điểm t. Chúng ta sẽ xác định hàm vị trí s(t) của vật, sau đó tính đạo hàm s'(t) để tìm vận tốc v(t). Cuối cùng, thay giá trị t vào v(t) để tìm vận tốc tại thời điểm đó.
Khi giải bài tập về đạo hàm, cần lưu ý các điểm sau:
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, bạn có thể tham khảo các bài tập tương tự sau:
Bài 7.30 trang 38 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán ứng dụng thực tế bằng phương pháp đạo hàm. Hy vọng với lời giải chi tiết và các lưu ý quan trọng trên, bạn sẽ nắm vững kiến thức và tự tin giải quyết bài tập này.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để khám phá thêm nhiều tài liệu học tập hữu ích và lời giải bài tập chi tiết.
| Công thức đạo hàm cơ bản | Ví dụ |
|---|---|
| (xn)' = nxn-1 | (x2)' = 2x |
| (sin x)' = cos x | (sin x)' = cos x |
| (cos x)' = -sin x | (cos x)' = -sin x |