Bài 4.8 trang 56 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về hàm số và đồ thị. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.8 trang 56, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’
Đề bài
Cho hình tứ diện SABC và các điểm A’,B’,C’ lần lượt thuộc các cạnh SA, SB, SC. Giả sử hai đường thẳng B’C’ và BC cắt nhau tại D, hai đường thẳng C’A’ và CA cắt nhau tại E và hai đường thẳng A’B’ và AB cắt nhau tại F. Chứng minh rằng ba điểm D, E, F thẳng hàng.
Phương pháp giải - Xem chi tiết
Chứng minh ba điểm đó cùng thuộc một đường thẳng (giao tuyến của hai mặt phẳng)
Lời giải chi tiết
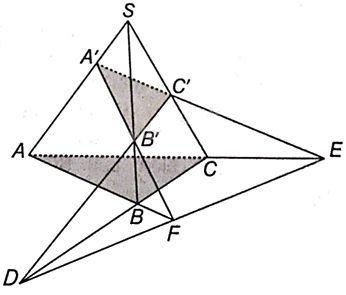
B’C’ và BC cắt nhau tại D nên D nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
C’A’ và CA cắt nhau tại E nên E nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
A’B’ và AB cắt nhau tại F nên F nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC).
Vậy D, E, F cùng nằm trên giao tuyến của hai mặt phẳng (A’B’C’) và (ABC) nên ba điểm này thẳng hàng.
Bài 4.8 trang 56 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán thuộc chủ đề hàm số bậc hai. Để giải bài toán này, học sinh cần nắm vững kiến thức về:
Nội dung bài toán:
(Giả sử nội dung bài toán là: Xác định parabol (P) đi qua ba điểm A(0;1), B(1;2), C(-1;0).)
Lời giải:
Giả sử parabol (P) có phương trình y = ax2 + bx + c.
Vì parabol (P) đi qua A(0;1) nên ta có: 1 = a(0)2 + b(0) + c => c = 1.
Vì parabol (P) đi qua B(1;2) nên ta có: 2 = a(1)2 + b(1) + c => a + b + c = 2. Thay c = 1, ta được a + b = 1.
Vì parabol (P) đi qua C(-1;0) nên ta có: 0 = a(-1)2 + b(-1) + c => a - b + c = 0. Thay c = 1, ta được a - b = -1.
Ta có hệ phương trình:
Cộng hai phương trình, ta được 2a = 0 => a = 0.
Thay a = 0 vào phương trình a + b = 1, ta được b = 1.
Vậy phương trình parabol (P) là y = 0x2 + 1x + 1 hay y = x + 1.
Kết luận:
Parabol (P) có phương trình y = x + 1.
Ngoài bài toán xác định parabol đi qua ba điểm, còn có nhiều dạng bài tập tương tự khác như:
Để giải các bài tập này, học sinh cần:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về hàm số bậc hai, học sinh có thể tham khảo thêm các bài tập sau:
Bài 4.8 trang 56 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và các ứng dụng của nó. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.