Bài 7.11 trang 28 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.11 trang 28, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) nhọn
Đề bài
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\), tam giác \(ABC\) nhọn. Gọi \(H,K\) lần lượt là trực tâm của tam giác \(ABC\) và \(SBC\). Chứng minh rằng:
a) \(BC \bot \left( {SAH} \right)\) và các đường thẳng \(AH,BC,SK\) đồng quy;
b) \(SB \bot \left( {CHK} \right)\) và \(HK \bot \left( {SBC} \right)\).
Phương pháp giải - Xem chi tiết
a) Chỉ ra \(BC \bot SA,BC \bot AH\) nên \(BC \bot \left( {SAH} \right)\).
Gọi \(M\) là giao điểm của \(AH\) và \(BC\)
Chứng minh \(BC \bot AH,BC \bot SM\) suy ra \(S,K,M\) thẳng hàng
Do đó, \(SK,AH,BC\) đồng quy tại \(M\).
b) Chỉ ra \(CH \bot SB\), \(SB \bot CK\) rồi suy ra \(SB \bot \left( {CHK} \right)\).
Từ đó ta có \(SB \bot HK\), tương tự, ta chứng minh được \(SC \bot \left( {BHK} \right)\), suy ra \(SC \bot HK\). Do đó \(HK \bot \left( {SBC} \right)\).
Lời giải chi tiết
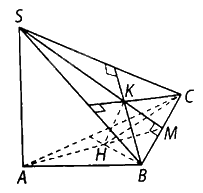
a) Chỉ ra \(BC \bot SA,BC \bot AH\) nên \(BC \bot \left( {SAH} \right)\).
Gọi \(M\) là giao điểm của \(AH\) và \(BC\)\(CH \bot AB\)
Ta có: \(BC \bot \left( {SAM} \right)\), suy ra \(BC \bot SM\), mà \(K\) là trực tâm của tam giác \(SBC\) nên \(SM\) đi qua \(K\).
Do đó, \(SK,AH,BC\) đồng quy tại \(M\).
b)
Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot CH\), mà , suy ra \(CH \bot \left( {SAB} \right)\).
Do đó \(CH \bot SB\), lại có \(SB \bot CK\) nên \(SB \bot \left( {CHK} \right)\).
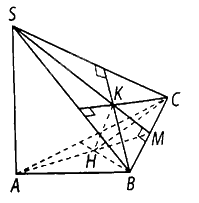
Từ đó ta có \(SB \bot HK\), tương tự, ta chứng minh được \(SC \bot \left( {BHK} \right)\), suy ra \(SC \bot HK\). Do đó \(HK \bot \left( {SBC} \right)\).
Bài 7.11 trang 28 sách bài tập Toán 11 - Kết nối tri thức là một bài toán ứng dụng đạo hàm để giải quyết một vấn đề thực tế. Để giải bài toán này, học sinh cần nắm vững các kiến thức về đạo hàm của hàm số, quy tắc tính đạo hàm, và cách sử dụng đạo hàm để tìm cực trị của hàm số.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Một vật chuyển động theo phương trình s(t) = t^3 - 3t^2 + 5t + 2. Tìm vận tốc và gia tốc của vật tại thời điểm t = 2.)
Để giải bài toán này, ta thực hiện các bước sau:
Trong bài toán này, hàm số mô tả vị trí của vật là s(t) = t^3 - 3t^2 + 5t + 2.
Vận tốc của vật là đạo hàm của hàm vị trí theo thời gian: v(t) = s'(t). Ta tính đạo hàm của s(t):
v(t) = s'(t) = 3t^2 - 6t + 5
Gia tốc của vật là đạo hàm của hàm vận tốc theo thời gian: a(t) = v'(t). Ta tính đạo hàm của v(t):
a(t) = v'(t) = 6t - 6
Thay t = 2 vào các công thức vận tốc và gia tốc:
v(2) = 3(2)^2 - 6(2) + 5 = 12 - 12 + 5 = 5
a(2) = 6(2) - 6 = 12 - 6 = 6
Vậy, vận tốc của vật tại thời điểm t = 2 là 5 đơn vị vận tốc, và gia tốc của vật tại thời điểm t = 2 là 6 đơn vị gia tốc.
Để củng cố kiến thức và kỹ năng giải bài tập về đạo hàm, các em có thể tham khảo các bài tập tương tự trong sách bài tập Toán 11 - Kết nối tri thức, hoặc tìm kiếm trên các trang web học toán online.
Khi giải bài tập về đạo hàm, các em cần chú ý:
Giaitoan.edu.vn là một nền tảng học Toán 11 online uy tín, cung cấp đầy đủ các bài giảng, bài tập, và lời giải chi tiết, giúp các em học sinh học Toán 11 hiệu quả. Chúng tôi cam kết mang đến cho các em trải nghiệm học tập tốt nhất.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài 7.11 trang 28 sách bài tập Toán 11 - Kết nối tri thức. Chúc các em học tập tốt!