Bài 4.44 trang 71 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến và tìm cực trị của hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.44 trang 71, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN
Đề bài
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và (P) là mặt phẳng cố định không song song với MN. Gọi A’, B’, C’, D’, M’, N’ lần lượt là hình chiếu của A, B, C, D, M, N qua phép chiếu lên mặt phẳng (P) theo phương MN.
a) Chứng minh rằng hai điểm M’ và N’ trùng nhau.
b) Chứng minh rằng bốn điểm A’, B’, C’, D’ là bốn đỉnh của một hình bình hành.
Phương pháp giải - Xem chi tiết
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
+ Nếu M thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
+ Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
Điểm M’ được gọi là hình chiếu của M trên mặt phẳng \(\left( \alpha \right)\) theo phương chiếu \(\Delta \).
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Lời giải chi tiết
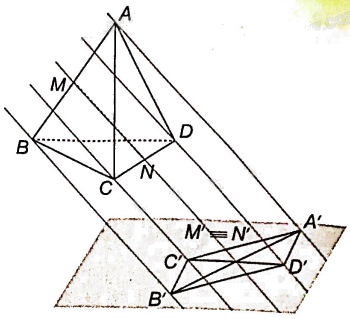
a) Vì đường thẳng MN là phương chiếu nên M’ của M trùng với hình chiếu N’ của N.
b) Vì M là trung điểm của AB nên theo tính chất của phép chiếu song song suy ra M’ là trung điểm của A’B’.
Vì N là trung điểm của CD nên theo tính chất của phép chiếu song song suy ra N’ là trung điểm của C’D’.
Vì M’ trùng N’ nên tứ giác tạo bởi bốn điểm A’, B’, C’, D’ có các đường chéo đi qua trung điểm của mỗi đường, suy ra tứ giác đó là hình bình hành.
Bài 4.44 trang 71 sách bài tập Toán 11 - Kết nối tri thức yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2.
Để tìm đạo hàm f'(x), ta áp dụng quy tắc đạo hàm của tổng và tích, cũng như quy tắc đạo hàm của lũy thừa:
Vậy, f'(x) = 3x2 - 6x.
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Suy ra x = 0 hoặc x = 2.
Vậy, hàm số có hai điểm cực trị tiềm năng là x = 0 và x = 2.
Để xác định khoảng đồng biến, nghịch biến, ta xét dấu đạo hàm f'(x):
Kết luận: Hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞), nghịch biến trên khoảng (0, 2).
Để tìm tọa độ các điểm cực trị, ta tính giá trị của hàm số tại các điểm x = 0 và x = 2:
Kết luận: Hàm số có điểm cực đại là (0, 2) và điểm cực tiểu là (2, -2).
Dựa vào các kết quả trên, ta có thể vẽ đồ thị hàm số f(x) = x3 - 3x2 + 2. Đồ thị hàm số sẽ có dạng đường cong đi lên từ âm vô cùng, đạt cực đại tại (0, 2), sau đó đi xuống đến cực tiểu tại (2, -2), và tiếp tục đi lên đến dương vô cùng.
Đồ thị hàm số cũng cho thấy tính chất đồng biến và nghịch biến của hàm số trên các khoảng khác nhau.
Bài 4.44 trang 71 sách bài tập Toán 11 - Kết nối tri thức là một bài tập điển hình về khảo sát hàm số bằng đạo hàm. Việc nắm vững các bước giải bài tập này sẽ giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của đạo hàm trong việc phân tích và vẽ đồ thị hàm số.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài tập và đạt kết quả tốt trong môn Toán 11.
Ngoài ra, các em có thể tham khảo thêm các bài giải khác trên giaitoan.edu.vn để nâng cao kiến thức và kỹ năng giải toán.
Để hiểu rõ hơn về đạo hàm và ứng dụng của đạo hàm, các em có thể xem lại các định nghĩa, tính chất và công thức liên quan trong sách giáo khoa và tài liệu tham khảo.
Chúc các em học tập tốt!