Bài 4.58 trang 73 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.58 trang 73 Sách bài tập Toán 11 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AA’, AB, AC
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N, P lần lượt là trung điểm của các cạnh AA’, AB, AC
a) Chứng minh rằng BC//(MNP).
b) Xác định giao tuyến d của hai mặt phẳng (MNP) và (A’B’C’)
c) Chứng minh rằng d//NP
Phương pháp giải - Xem chi tiết
+ Nếu đường thẳng a không nằm trong mặt phẳng (P) và a song song với một đường thẳng nằm trong mặt phẳng (P) thì a song song với (P).
+ Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
+ Để tìm giao tuyến của hai mặt phẳng, ta đi tìm hai điểm chung thuộc cả hai mặt phẳng đó rồi nối hai điểm chung đó lại ta được giao tuyến cần tìm.
Lời giải chi tiết
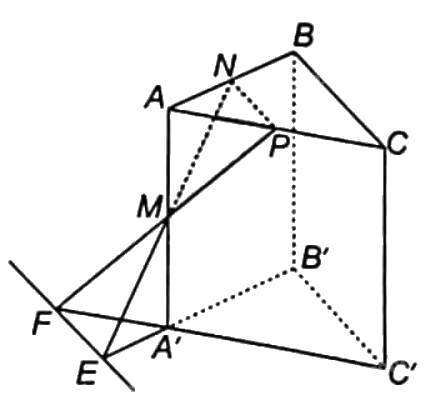
a) Vì NP là đường trung bình của tam giác ABC nên BC//NP, suy ra BC//(MNP).
b) Trong mặt phẳng (ABB’A’), gọi E là giao điểm của MN và A’B’. Trong mặt phẳng (ACC’A’) gọi F là giao điểm của MP và A’C’. Khi đó, EF là giao tuyến của hai mặt phẳng (MNP) và (A’B’C’).
c) Vì BC//NP và BC//B’C’ nên NP//B’C’, suy ra NP//(A’B’C’). Mặt phẳng (MNP) chứa đường thẳng NP//(A’B’C’) nên giao tuyến d của hai mặt phẳng đó song song với B’C’, suy ra d//NP.
Bài 4.58 trang 73 Sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về đường thẳng và mặt phẳng trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản như:
Dưới đây là lời giải chi tiết bài 4.58 trang 73 Sách bài tập Toán 11 - Kết nối tri thức:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông cạnh a nên AC = BD = a√2. Do đó, AO = BO = CO = DO = a√2 / 2.
Vì SA vuông góc với mặt phẳng (ABCD) nên SA vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABCD), đặc biệt là SA vuông góc với AC.
Xét tam giác SAC vuông tại A, ta có:
tan(∠SCA) = SA / AC = a / (a√2) = 1/√2
Suy ra ∠SCA = arctan(1/√2) ≈ 35.26°
Gọi φ là góc giữa đường thẳng SC và mặt phẳng (ABCD). Ta có:
φ = ∠SCA = arctan(1/√2) ≈ 35.26°
Vậy, góc giữa đường thẳng SC và mặt phẳng (ABCD) là khoảng 35.26°.
Trong quá trình giải bài tập, học sinh cần chú ý các bước sau:
Để củng cố kiến thức về đường thẳng và mặt phẳng trong không gian, học sinh có thể tham khảo các bài tập tương tự sau:
Bài 4.58 trang 73 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập điển hình về ứng dụng kiến thức về đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về bài tập này và tự tin giải các bài tập tương tự.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!