Bài 4.41 trang 71 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.41 trang 71, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho \(MB = 2MC.\)
Đề bài
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M là điểm thuộc cạnh BC sao cho \(MB = 2MC.\)
a) Xác định hình chiếu M’ của M qua phép chiếu song song lên mặt phẳng (A’B’C’) theo phương AA’.
b) Chứng minh rằng \(M'B' = 2M'C'\)
Phương pháp giải - Xem chi tiết
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(\Delta \) cắt \(\left( \alpha \right)\). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
+ Nếu M thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và \(\Delta \).
+ Nếu M không thuộc \(\Delta \) thì M’ là giao điểm của \(\left( \alpha \right)\) và đường thẳng qua M song song với \(\Delta \).
Điểm M’ được gọi là hình chiếu của M trên mặt phẳng \(\left( \alpha \right)\) theo phương chiếu \(\Delta \).
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó; phép chiếu song song giữa nguyên tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.
Lời giải chi tiết
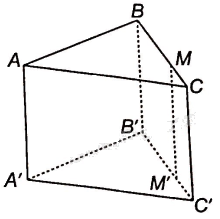
a) Trong mặt phẳng (BCC’B’) vẽ MM’//BB’ (M’ thuộc B’C’) thì M’ là hình chiếu của M qua phép chiếu đã cho.
b) Vì AA’//BB’//CC’ nên B’, C’ lần lượt là hình chiếu của B, C lên mặt phẳng (A’B’C’) theo phương chiếu AA’. Theo tính chất của phép chiếu song song suy ra \(\frac{{M'B'}}{{M'C'}} = \frac{{MB}}{{MC}} = 2\), suy ra \(M'B' = 2M'C'\)
Bài 4.41 trang 71 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài toán thuộc chương trình hình học không gian, cụ thể là phần đường thẳng và mặt phẳng trong không gian. Để giải bài toán này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài toán: (Giả sử bài toán yêu cầu tìm góc giữa đường thẳng và mặt phẳng, hoặc chứng minh sự song song, vuông góc giữa chúng. Nội dung cụ thể của bài toán sẽ được thay thế vào đây)
Lời giải chi tiết:
Ví dụ minh họa: (Cung cấp một ví dụ cụ thể về cách giải bài toán tương tự, với các số liệu và kết quả cụ thể)
Lưu ý quan trọng:
Mở rộng kiến thức:
Các bài toán về đường thẳng và mặt phẳng trong không gian có nhiều ứng dụng thực tế trong các lĩnh vực như kiến trúc, xây dựng, kỹ thuật,... Việc nắm vững kiến thức về chủ đề này sẽ giúp bạn giải quyết các bài toán phức tạp hơn và ứng dụng vào thực tế một cách hiệu quả.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu học tập khác như sách giáo khoa, sách bài tập, các trang web học toán online để củng cố kiến thức và rèn luyện kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc các bạn học tập tốt!
Các bài toán tương tự: