Bài 7.50 trang 42 sách bài tập Toán 11 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình hộp ABCD.A’B’C’D’, gọi M là trung điểm của AA’.
Đề bài
Cho hình hộp ABCD.A’B’C’D’, gọi M là trung điểm của AA’. Tỷ số của thể tích khối chóp M.ABCD và khối hộp ABCD.A’B’C’D’ bằng
A. \(\frac{1}{3}\).
B. \(\frac{1}{2}\).
C. \(\frac{1}{6}\).
D. \(\frac{2}{3}\).
Phương pháp giải - Xem chi tiết
Nhận xét \(MA = \frac{1}{2}A'A \Rightarrow d\left( {M,\left( {ABCD} \right)} \right) = \frac{1}{2}d\left( {A',\left( {ABCD} \right)} \right)\)
Áp dụng công thức tính thể tích khối chóp và khối lăng trụ
Suy ra \(\frac{{{V_{M.ABCD}}}}{{{V_{ABCD.A'B'C'D'}}}}\)
Lời giải chi tiết
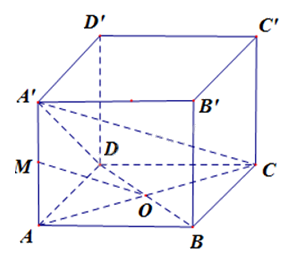
\(MA = \frac{1}{2}A'A \Rightarrow d\left( {M,\left( {ABCD} \right)} \right) = \frac{1}{2}d\left( {A',\left( {ABCD} \right)} \right)\)
\({V_{M.ABCD}} = \frac{1}{3}d\left( {M,\left( {ABCD} \right)} \right).{S_{ABCD}} = \frac{1}{3}.\frac{1}{2}d\left( {A',\left( {ABCD} \right)} \right).{S_{ABCD}} = \frac{1}{6}{V_{ABCD.A'B'C'D'}}\)
Tỉ số \(\frac{{{V_{M.ABCD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \frac{1}{6}\)
Bài 7.50 yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị. Để giải bài này, chúng ta cần nắm vững các bước sau:
Để minh họa, chúng ta sẽ xét một ví dụ cụ thể. Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2.
| Khoảng | x < 0 | 0 < x < 2 | x > 2 |
|---|---|---|---|
| f'(x) | + | - | + |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Ngoài bài 7.50, các em học sinh có thể luyện tập thêm các bài tập tương tự để củng cố kiến thức về khảo sát hàm số. Các bài tập này thường yêu cầu các em áp dụng các bước tương tự như trên, nhưng với các hàm số khác nhau. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải các bài tập khó hơn.
Đạo hàm và khảo sát hàm số là một trong những chủ đề quan trọng nhất trong chương trình Toán 11. Việc hiểu rõ các khái niệm và kỹ năng liên quan đến đạo hàm và khảo sát hàm số sẽ giúp các em học sinh:
Bài 7.50 trang 42 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể tại giaitoan.edu.vn, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.