Bài 3.3 trang 46 sách bài tập Toán 11 thuộc chương trình học Toán 11 Kết nối tri thức với cuộc sống. Bài tập này thường xoay quanh các kiến thức về vectơ, phép toán vectơ, và ứng dụng của vectơ trong hình học.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Trẻ sơ sinh được xem là nhẹ cân nếu cân nặng khi sinh dưới 2kg, là thừa cân nếu cân nặng trên 4kg, là có cân nặng trung bình nếu cân nặng khi sinh từ 2kg đến 4kg.
Đề bài
Trẻ sơ sinh được xem là nhẹ cân nếu cân nặng khi sinh dưới 2kg, là thừa cân nếu cân nặng trên 4kg, là có cân nặng trung bình nếu cân nặng khi sinh từ 2kg đến 4kg. Thống kê cân nặng (tính theo kg) của 15 trẻ sơ sinh tại một bệnh viện cho kết quả như sau:
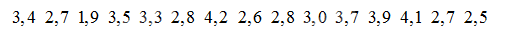
a) Tìm số trẻ nhẹ cân, thừa cân, có cân nặng trung bình trong 15 trẻ sơ sinh trên.
b) Xây dựng mẫu số liệu ghép nhóm cho mẫu số liệu trên.
Phương pháp giải - Xem chi tiết
Để chuyển mẫu số liệu không ghép nhóm sang mẫu số liệu ghép nhóm ta thực hiện như sau:
Bước 1: Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước.
Bước 2: Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng thống kê cho mẫu số liệu ghép nhóm
Trong các bài tập, ta không nên chia thành quá nhiều hoặc quá ít nhóm. Các nhóm không giao nhau và nên có độ dài bằng nhau, tổng độ dài các nhóm lớn hơn khoảng biến thiên.
Lời giải chi tiết
a) Số trẻ nhẹ cân, cân nặng trung bình, thừa cân tương ứng là 1, 12, 2.
b) Mẫu số liệu ghép nhóm:

Bài 3.3 trang 46 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng. Dưới đây là hướng dẫn giải chi tiết từng phần của bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết cơ bản:
Để giải bài 3.3 trang 46, chúng ta cần phân tích đề bài và xác định các yếu tố quan trọng. Thông thường, bài tập sẽ yêu cầu:
Ví dụ, một bài tập có thể yêu cầu:
Cho hai điểm A(xA, yA) và B(xB, yB). Tìm tọa độ của vectơ AB.
Lời giải:
Tọa độ của vectơ AB được tính theo công thức: AB = (xB - xA, yB - yA)
Để nắm vững kiến thức và kỹ năng giải bài tập về vectơ, bạn nên luyện tập thêm với các bài tập tương tự. Dưới đây là một số bài tập gợi ý:
Kiến thức về vectơ có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, như vật lý, kỹ thuật, đồ họa máy tính. Ví dụ:
Khi giải bài tập về vectơ, bạn cần lưu ý một số điều sau:
Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải thành công bài 3.3 trang 46 sách bài tập Toán 11 - Kết nối tri thức với cuộc sống. Chúc bạn học tốt!
| Công thức | Mô tả |
|---|---|
| AB = (xB - xA, yB - yA) | Tọa độ của vectơ AB |
| a.b = |a||b|cos(θ) | Tích vô hướng của hai vectơ a và b |