Bài 4.1 trang 55 sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số và đồ thị để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.1 trang 55, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Gọi M là một điểm bất kì thuộc cạnh SC.
Đề bài
Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Gọi M là một điểm bất kì thuộc cạnh SC.
a) Xác định giao tuyến của hai mặt phẳng (AMO) và (SCD).
b) Xác định giao tuyến của hai mặt phẳng (BMO) và (SCD).
Phương pháp giải - Xem chi tiết
Để xác định giao tuyến của hai mặt phẳng, ta tìm hai điểm chung (phân biệt) của hai mặt phẳng đó.
Lời giải chi tiết
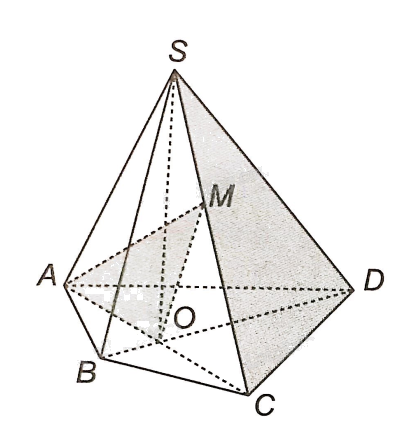
a) Ta thấy M thuộc AM, nằm trong mặt phẳng (AMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (AMO) và (SCD).
Ta thấy C thuộc đường thẳng AC (trùng với đường thẳng AO nên nó nằm trong mặt phẳng (AMO). C lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy C là điểm chung thứ hai của (AMO) và (SCD).
Vậy nên MC (hay SC) là giao tuyến của hai mặt phẳng (AMO) và (SCD).
b) Ta thấy M thuộc BM, nằm trong mặt phẳng (BMO). M lại thuộc SC, nằm trong mặt phẳng (SCD). Vậy M là điểm chung thứ nhất của (BMO) và (SCD).
Ta thấy D thuộc đường thẳng BD (trùng với đường thẳng BO nên nó nằm trong mặt phẳng (BMO). D lại thuộc SD, nằm trong mặt phẳng (SCD). Vậy D là điểm chung thứ hai của (BMO) và (SCD).
Vậy nên MD là giao tuyến của hai mặt phẳng (BMO) và (SCD).
Bài 4.1 trang 55 sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Dưới đây là đề bài và lời giải chi tiết bài 4.1 trang 55 sách bài tập Toán 11 - Kết nối tri thức:
Xác định parabol (P) trong mỗi trường hợp sau:
Hàm số y = 2x2 - 3x + 1 là một hàm số bậc hai với a = 2, b = -3, c = 1.
Hoành độ đỉnh: x0 = -b / (2a) = -(-3) / (2 * 2) = 3/4
Tung độ đỉnh: y0 = 2 * (3/4)2 - 3 * (3/4) + 1 = 2 * (9/16) - 9/4 + 1 = 9/8 - 18/8 + 8/8 = -1/8
Vậy đỉnh của parabol là I(3/4; -1/8).
Trục đối xứng là đường thẳng x = 3/4.
Thay x = 0 vào phương trình hàm số, ta được y = 1. Vậy giao điểm với trục tung là A(0; 1).
Giải phương trình 2x2 - 3x + 1 = 0. Ta có: Δ = (-3)2 - 4 * 2 * 1 = 9 - 8 = 1 > 0
x1 = (3 + √1) / (2 * 2) = (3 + 1) / 4 = 1
x2 = (3 - √1) / (2 * 2) = (3 - 1) / 4 = 1/2
Vậy giao điểm với trục hoành là B(1; 0) và C(1/2; 0).
(Tương tự như phần a, thực hiện các bước tính toán để xác định đỉnh, trục đối xứng, giao điểm với trục tung và trục hoành)
(Tương tự như phần a, thực hiện các bước tính toán để xác định đỉnh, trục đối xứng, giao điểm với trục tung và trục hoành)
Kết luận:
Việc xác định các yếu tố của parabol giúp chúng ta hiểu rõ hơn về hình dạng và vị trí của đồ thị hàm số bậc hai. Bài tập 4.1 trang 55 sách bài tập Toán 11 - Kết nối tri thức là một bài tập cơ bản nhưng quan trọng, giúp học sinh rèn luyện kỹ năng giải toán và áp dụng kiến thức vào thực tế.
Hy vọng với lời giải chi tiết này, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán 11.
Để học thêm nhiều bài tập và kiến thức Toán 11, các em có thể truy cập website giaitoan.edu.vn để được hỗ trợ.