Bài 4.31 trang 67 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đường thẳng và mặt phẳng trong không gian để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.31 trang 67, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E là một điểm bất kì thuộc cạnh SA và (P) là mặt phẳng qua E song song với mặt phẳng (ABCD).
a) Xác định giao tuyến của mặt phẳng (P) và các mặt bên của hình chóp.
b) Hình tạo bởi các giao tuyến là hình gì? Giải thích vì sao.
Phương pháp giải - Xem chi tiết
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a song song với b.
Cho hai mặt phẳng song song, nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết
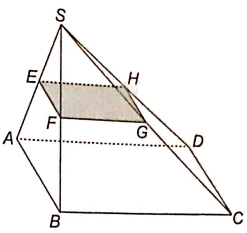
a) Trong mặt phẳng (SAB), qua E kẻ đường thẳng song song với AB cắt SB tại F. Khi đó, EF là giao tuyến của mặt phẳng (P) và mặt phẳng (SAB).
Trong mặt phẳng (SBC), qua F kẻ đường thẳng song song với BC cắt SC tại G. Khi đó, FG là giao tuyến của mặt phẳng (P) và mặt phẳng (SBC).
Trong mặt phẳng (SCD), qua G kẻ đường thẳng song song với DC cắt SD tại H. Khi đó, GH là giao tuyến của mặt phẳng (P) và mặt phẳng (SCD).
Vì E vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (SAD); H vừa thuộc mặt phẳng (P) vừa thuộc mặt phẳng (SAD) nên EH là giao tuyến của (P) và mặt phẳng (SAD)
b) Vì mp (ABCD)//mp (EFGH), EH là giao tuyến của mp (EFGH) và mp (SAD), AD là giao tuyến của mp (ABCD) và mp (SAD) nên EH//AB.
Vì EH//AD, AD//BC nên EH//BC
Mà FG//BC nên EH//FG
Vì EF//AB, AB//CD nên EF//DC
Mà HG//DC nên EF//HG
Tứ giác EFGH có: EF//GH, EH//FG nên tứ giác EFGH là hình bình hành.
Bài 4.31 trang 67 sách bài tập Toán 11 Kết nối tri thức thuộc chương 3: Đường thẳng và mặt phẳng trong không gian. Bài toán này thường liên quan đến việc xác định mối quan hệ giữa đường thẳng và mặt phẳng, sử dụng các định lý và tính chất đã học để chứng minh hoặc tính toán.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Đồng thời, cần nhớ lại các kiến thức liên quan như:
(Nội dung lời giải chi tiết bài 4.31 trang 67 sẽ được trình bày tại đây. Lời giải cần bao gồm các bước giải rõ ràng, sử dụng các ký hiệu toán học chính xác và giải thích chi tiết từng bước để người học dễ hiểu. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu chứng minh đường thẳng d vuông góc với mặt phẳng (P). Lời giải có thể như sau:
Ngoài bài 4.31, còn rất nhiều bài tập tương tự trong sách bài tập Toán 11 Kết nối tri thức. Các bài tập này thường có dạng:
Để giải các bài tập này, chúng ta có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tự giải các bài tập sau:
Bài 4.31 trang 67 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp các em học sinh hiểu rõ hơn về mối quan hệ giữa đường thẳng và mặt phẳng trong không gian. Hy vọng với lời giải chi tiết và các hướng dẫn trên, các em sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!