Bài 1.21 trang 18 Sách bài tập Toán 11 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.21 trang 18 Sách bài tập Toán 11 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Từ đồ thị hàm số \(y = \cos {\rm{ }}x\), hãy vẽ các đồ thị hàm số sau:
Đề bài
Từ đồ thị hàm số \(y = \cos {\rm{ }}x\), hãy vẽ các đồ thị hàm số sau:
a) \(y = \, - \cos {\rm{ }}x\);
b) \(y = \,|\cos {\rm{ }}x|\);
c) \(y = \cos {\rm{ }}x + 1\);
d) \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\).
Phương pháp giải - Xem chi tiết
Từ đồ thị \(y = \cos {\rm{ }}x\), ta linh hoạt dịch chuyển đồ thị theo yêu cầu đề bài. Vẽ đồ thị \(y = \cos {\rm{ }}x\) bằng nét đứt và vẽ đồ thị trong đề bài bằng nét liền.
Lời giải chi tiết
a) Lấy đối xứng đồ thị hàm số \(y = \cos {\rm{ }}x\) qua trục hoành, ta được đồ thị hàm số \(y = \, - \cos {\rm{ }}x\).
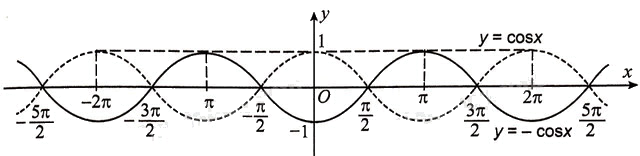
Trong hình trên, đồ thị hàm số \(y = \cos {\rm{ }}x\) là đường nét đứt còn đồ thị hàm số \(y = \, - \cos {\rm{ }}x\) là đường nét liền.
b) Ta có
\(y = \,|\cos {\rm{ }}x|\, = \left\{ \begin{array}{l}\cos x\,\,\,\,\,\,{\rm{khi}}\,\,\,\cos x \ge 0\\ - \cos x\,\,{\rm{khi}}\,\,\,\cos x < 0\end{array} \right.\)
Từ đó, để vẽ đồ thị hàm số \(y = \,|\cos {\rm{ }}x|\) ta vẽ đồ thị hàm số \(y = \cos {\rm{ }}x\) ở phía trên trục Ox và lấy đối xứng qua trục Ox phần đồ thị hàm số \(y = \cos {\rm{ }}x\) ở phía dưới trục Ox. Trong hình trên, đồ thị hàm số \(y = \cos {\rm{ }}x\) là đường nét đứt còn đồ thị hàm số \(y = \,|\cos {\rm{ }}x|\) là đường nét liền.
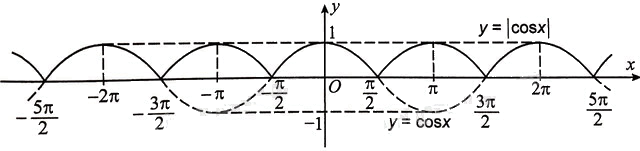
c) Để vẽ hàm số \(y = \cos {\rm{ }}x + 1\) đầu tiên ta vẽ hàm số \(y = \cos {\rm{ }}x\), sau đó dịch chuyển đồ thị này dọc theo trục Oy lên phía trên 1 đơn vị, ta được đồ thị hàm số. Trong hình dưới đây, đồ thị hàm số \(y = \cos {\rm{ }}x + 1\) là đường nét liền.
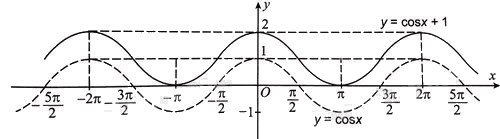
d) Để vẽ hàm số \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\) đầu tiên ta vẽ hàm số \(y = \cos {\rm{ }}x\), sau đó dịch chuyển đồ thị này dọc theo trục Ox sang bên trái \(\frac{\pi }{2}\) đơn vị, ta được đồ thị hàm số. Trong hình dưới đây, đồ thị hàm số \(y = \,\cos \left( {x + \frac{\pi }{2}} \right)\) là đường nét liền.
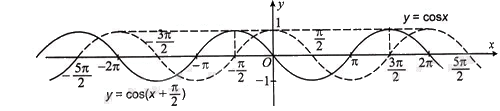
Bài 1.21 trang 18 Sách bài tập Toán 11 - Kết nối tri thức thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:
Nội dung bài tập 1.21: Bài tập yêu cầu chứng minh một đẳng thức vectơ hoặc tìm một vectơ thỏa mãn một điều kiện cho trước. Thông thường, để giải quyết bài tập này, học sinh cần:
Lời giải chi tiết bài 1.21:
(Ở đây sẽ là lời giải chi tiết của bài 1.21, bao gồm các bước giải, giải thích rõ ràng và các ví dụ minh họa. Lời giải sẽ được trình bày một cách logic và dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải toán.)
Ví dụ minh họa:
Giả sử bài toán yêu cầu chứng minh rằng AB + CD = AD + CB. Để chứng minh đẳng thức này, ta có thể sử dụng quy tắc hình bình hành:
Mở rộng kiến thức:
Ngoài bài 1.21, còn rất nhiều bài tập tương tự trong Sách bài tập Toán 11 - Kết nối tri thức. Để nắm vững kiến thức và kỹ năng giải toán, học sinh nên:
Lưu ý khi giải bài tập về vectơ:
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 1.21 trang 18 Sách bài tập Toán 11 - Kết nối tri thức sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!
Các bài tập liên quan: