Bài 7.7 trang 28 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải bài 7.7 trang 28 ngay dưới đây!
Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đôi một vuông góc với nhau.
Đề bài
Cho tứ diện \(OABC\) có ba cạnh \(OA,OB,OC\) đôi một vuông góc với nhau. Gọi \(H\) là chân đường vuông góc hạ từ \(O\) đến mặt phẳng\(\left( {ABC} \right)\). Chứng minh rằng:
a)\(BC \bot \left( {OAH} \right)\);
b) \(H\) là trực tâm của tam giác \(ABC\);
c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng
một mặt phẳng thì nó vuông góc với mặt phẳng đó.
+ \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \subset \alpha \end{array} \right. \Rightarrow a \bot b\)
a) Chứng minh \(OA \bot BC\), \(OH \bot BC\).
b) Chứng minh \(BC \bot AH\), \(CA \bot BH\) suy ra \(H\) là trực tâm của tam giác \(ABC\).
c) + Gọi \(K\) là giao điểm của \(AH\) và \(BC\),
+ Chứng minh \(OK\) là đường cao của tam giác vuông \(OBC\) và \(OH\) là đường cao của tam giác vuông \(OAK\).
+ Áp dụng hệ thức lượng trong các tam giác vuông \(OBC\) và \(OAK\)
Lời giải chi tiết
a) Vì \(OA \bot OB,OA \bot OC \Rightarrow OA \bot \left( {OBC} \right)\), suy ra. \(OA \bot BC\)
Vì \(OH \bot \left( {ABC} \right)\) nên\(OH \bot BC\),suy ra\(BC \bot \left( {OAH} \right)\).
b) Vì \(BC \bot \left( {OAH} \right)\) nên \(BC \bot AH\).
Tương tự, \(CA \bot BH\), do đó \(H\) là trực tâm của tam giác\(ABC\).
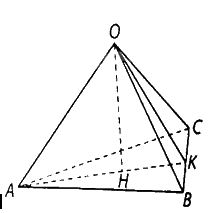
c) Gọi \(K\) là giao điểm của \(AH\) và \(BC\),
Ta có: \(OK \bot BC\) và \(OA \bot OK\) nên \(OK\) là đường cao của tam giác vuông \(OBC\) và là đường cao của tam giác vuông \(OAK\).
Áp dụng hệ thức lượng trong các tam giác vuông \(OBC\) và\(OAK\), ta có: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{K^2}}}\) và \(\frac{1}{{O{K^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Từ đó suy ra: \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Bài 7.7 trang 28 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các bước sau:
Giả sử bài toán yêu cầu tìm giá trị lớn nhất của hàm số f(x) = -x2 + 4x - 3 trên đoạn [0; 3].
| x | 0 | 2 | 3 |
|---|---|---|---|
| f'(x) | + | 0 | - |
| f(x) | -3 | 1 | 0 |
Ngoài bài 7.7 trang 28, sách bài tập Toán 11 Kết nối tri thức còn nhiều bài tập tương tự về ứng dụng đạo hàm để giải quyết các bài toán tối ưu. Các dạng bài tập này thường yêu cầu học sinh:
Để giải quyết các bài tập này, học sinh cần:
Khi giải các bài tập về đạo hàm, học sinh cần lưu ý một số điểm sau:
Bài 7.7 trang 28 sách bài tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Bằng cách nắm vững các bước giải và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.